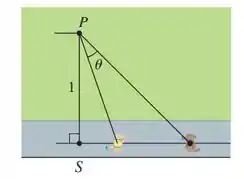
Um observador permanece em um ponto , distante uma unidade de uma pista. Dois corredores iniciam no ponto da figura e correm ao longo da pista. Um corredor corre três vezes mais rápido que o outro. Encontre o valor máximo do ângulo de visão do observador entre os corredores. [Sugestão: Maximize .]
Passo 1
Fala aí, tudo belezinha?
Bom, essa questão diz pra gente que há um observador num ponto , e dois corredores iniciam no ponto da figura e correm ao longo da pista. Um corredor corre três vezes mais rápido que o outro.
Devemos encontrar o valor máximo do ângulo de visão do observador entre os corredores.
Além disso o enunciado dá pra gente a sugestão de maximizar .
Então é isso que faremos.
Mas para isso precisamos descrever essa situação em termos da . Para isso, vamos primeiro desenhar a situação.
E depois usaremos a derivada igualada a zero para a maximização que estamos querendo.
Então vamos nessa.
Passo 2
Podemos começar esboçando a situação. Veja que:
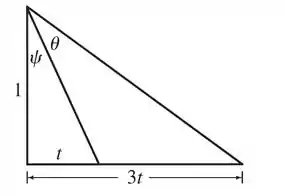
Precisamos maximizar a tangente de , para isso usaremos essa relação trigonométrica diretamente do triângulo, para posteriormente isolarmos . Assim:
E podemos escrever:
Então, multiplicando cruzando, ficamos com:
E isolando a
Passo 3
Vamos chamar de , então, maximizando encontrando sua derivada.
Assim,
Que se torna:
E usando a regra do quociente, teremos:
Que pode ser escrita com:
E igualando tudo a zero, teremos:
Como o denominador nunca pode ser zero, basta fazer:
Assim:
E teremos:
Passo 4
Agora, substituindo na tangente de , temos:
O ângulo que tem é o ângulo
Resposta
O valor máximo do ângulo é