Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 30

obtenha um campo de direção e trace o gráfico da solução particular ao longo do intervalo especificado. Use seu solucionador SAC para equações diferenciais para encontrar a solução geral da equação diferencial.

y ' = s e n   x ⋅ s e n   y ,     y 0 = 2

- 6 ≤ x ≤ 6 ,     - 6 ≤ y ≤ 6

Passo 1

Devemos resolver a equação diferencial ordinária e depois plotar o campo de direções e plotar a solução particular junto. Primeiramente devemos lembrar que y ' = d y / d x e assim poderemos escrever nossa equação separando tudo que tem x de um lado e tudo que tem y do outro

d y d x = s e n   x ⋅ s e n   y

d y s e n   y = s e n   x   d x

Passo 2

Agora, podemos aplicar a integral em ambos os lados e obteremos

∫ d y s e n   y = ∫ s e n   x   d x

Resolveremos cada uma das integrais separadamente e depois vamos juntar em único resultado. Assim,

i ∫ s e n   x   d x =   - cos ⁡ x + C 1

i i   ∫ d y s e n   y =   - ln ⁡ c o s s e c y + cot ⁡ y + C 2

Sendo k = C 1 - C 2

- cos ⁡ x + C 1 = - ln ⁡ c o s s e c y + cot ⁡ y + C 2

- ln ⁡ c o s s e c y + cot ⁡ y = - cos ⁡ x + C 1 - C 2

- ln ⁡ c o s s e c y + cot ⁡ y =   - cos ⁡ x   + K

Utilizando a condição inicial y 0 = 2

- ln ⁡ c o s s e c 2 + cot ⁡ 2 =   - cos ⁡ 0   + K

- ln ⁡ c o s s e c 2 + cot ⁡ 2 =   - 1 + K

k = 1 - ln ⁡ c o s s e c 2 + cot ⁡ 2

Nossa Solução particular vai ser

- ln ⁡ c o s s e c y + cot ⁡ y =   - cos ⁡ x   + 1 - ln ⁡ c o s s e c 2 + cot ⁡ 2

Passo 3

Por fim, utilizando um software de plotagem de gráficos vamos plotar o campo de direções para essa equação diferencial

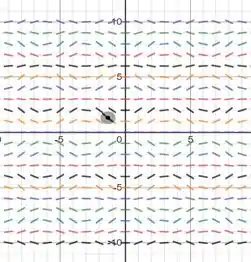
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que população cresça de acordo com o modelo logístico com uma população inicial de 1000 e capacidade de suporte 1000. Se a população crescer para 2500 após um ano, como será a população após o
Suponha que uma população P(t) satisfaça d P d t = 0,4 P - 0,001 P 2 P 0 = 50 Onde t é medido em anos.(a) Qual a capacidade de suporte?(b) O que é P’(0)?(c) Quando a população atingirá 50% da capacida
11. Determine uma curva que passa pelo ponto ( 0,2 ) e que goza da propriedade: a reta tangente no ponto ( x , y ) encontra o eixo x no ponto A , de abscissa 0 , de tal modo que a distância de ( x , y
Resolva a equação diferencial. d y d x = x e y
Resolva a equação diferencial. d y d x = y x