Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 28

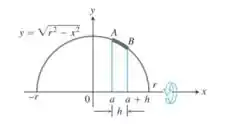
Você sabia que se cortar um filão de pão esférico em fatias de igual largura cada fatia terá a mesma quantidade de casca? Para saber o porquê disso, suponha que o semicírculo y = r 2 - x 2 mostrado a seguir girado em torno do eixo x para gerar uma esfera. Seja A B um arco desse semicírculo que se encontra acima de um intervalo de comprimento h no eixo x . Demonstre que a área gerada por A B não depende da localização do intervalo. (Depende apenas do comprimento do intervalo.)

Passo 1

Para essa questão calcularemos a área da curva dada em torno do eixo x , considerando os limites de integração como a   e   a + h , ou seja, o comprimento do intervalo. A área da superfície gerada ao rotacionar a curva em torno do eixo x é dada por:

S = ∫ a b 2 π f x 1 + f ' x 2   d x

Assim, temos que:

S = ∫ a a + h 2 π r 2 - x 2   1 + - x r 2 - x 2 2 d x =  

=   2 π ∫ a a + h r 2 - x 2   r 2 - x 2 + x 2 r 2 - x 2   d x = 2 π ∫ a a + h r   d y = 2 π r y a + h a =

= 2 π r a + h - a = 2 π r h

Portanto o resultado final mostra que a área gerada por A B   depende somente de h que é o comprimento do intervalo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.b) f x = R 2 - x 2 , - R ≤ x ≤ RR0
Calcule a área da superfície gerada pela rotação, em torno do eixox, do gráfico da função dada: f x = e x + e - x 2 ,- 1 ≤ x ≤ 1
Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.c) f x = x 2 , 0 ≤ x1 2
Para x = s e n( y ) ,0 ≤ y ≤ π ; eixo y :Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.Trace o gráfico da curva para ver como ela é. Se puder
Para x 1 2 + y 1 2 = 3 ,d e4,1a( 1,4 ) ; eixo x :Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.Trace o gráfico da curva para ver como ela é.