Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 44

Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

44-

y = 5 x 4 + 5

Passo 1

Fazendo a derivada primeira teremos:

y ' = 5 ' x 4 + 5 - 5 ( x 4 + 5 ) ' x 4 + 5 2

y ' = 0 - 20 x 3 x 4 + 5 2

Agora fazendo a segunda derivada:

y ' ' = - 20 x 3 ' x 4 + 5 2 - ( - 20 x 3 ) ( x 4 + 5 2 ) ' ) x 4 + 5 4

y ' ' = - 60 x 2 x 4 + 5 2 + 20 x 3 × 2 ( x 4 + 5 ) ( 4 x 3 ) x 4 + 5 4

y ' ' = x 4 + 5 [ - 60 x 2 x 4 + 5 + 40 x 3 ( 4 x 3 ) x 4 + 5 4

y ' ' = - 60 x 6 - 300 x 2 + 160 x 6 x 4 + 5 3 ∴ 100 x 6 - 300 x 2 x 4 + 5 3 ∴ 100 x 2 ( x 4 - 3 ) x 4 + 5 3

Passo 2

Analisando y’ para encontrarmos os pontos críticos:

y ' = 0 →   - 20 x 3 = 0 → x = 0

Tal como a função, a derivada primeira não tem como o denominador ser negativo, por ter raízes imaginarias .

Passo 3

Agora precisamos verificar y ' ' e ver se os pontos encontrados são máximos ou mínimos e se temos pontos de inflexão .

y ' ' 0 = 100 ( 0 ) 2 ( 0 4 - 3 ) 0 4 + 5 3 = 0

Então não podemos afirmar sobre x = 0

Para acharmos pontos de inflexão:

100 x 2 x 4 - 3 = 0

Para ser 0 essa equação pode ter os seguintes valores de x :

x = 0 ;               x = ± 3 4

Para saber o que é x = 0 somente fazendo a tabela para ver.

Passo 4

Agora precisamos descobrir as assíntotas horizontais:

lim x → ∞ ⁡ 5 x 4 + 5 → 5 ∞ = 0

lim x → - ∞ ⁡ 5 x 4 + 5 → 5 - ∞ = 0

Logo a assíntota da função é y=0. Isso é em valores extremos a função retorna valor 0.

Passo 5

Agora arrumando os intervalos temos:

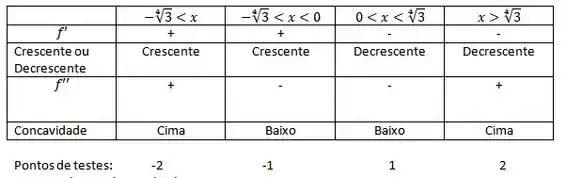
Logo x=0 é um máximo absoluto.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um computador para traçar o gráfico de f e para achar f 'ef ' ' . Use estes gráficos para estimar os intervalos crescentes e decrescentes, valores extremos, intervalos de concavidade e pontos de i
(a) Encontre os intervalos de aumento ou diminuição.(b) Encontre os valores máximos e mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as informações das partes
Uma partícula se move com s = f t ,t ≥ 0 : f t = 9 t t 2 + 9 Encontre a velocidadeEncontre a velocidade para t = 1 Quando a partícula está em repouso?Quando a particula se move na direção positiva?Qua
Uma partícula se move com s = f t ,t ≥ 0 : f t = t 3 - 8 t 2 + 24 t Encontre a velocidadeEncontre a velocidade para t = 1 Quando a partícula está em repouso?Quando a particula se move na direção posit
Uma partícula se move com s = f t ,t ≥ 0 : f t = s e n π t 2 Encontre a velocidadeEncontre a velocidade para t = 1 Quando a partícula está em repouso?Quando a particula se move na direção positiva?Qua