Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 45

Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

45-

Passo 1

Por ser uma função dentro de um módulo precisamos desmembrar essa função em duas, que é como funciona a função módulo onde a parte negativa reflete e vira positiva.

Onde uma função é uma função caso a parte dentro do módulo seja negativa e outra zero ou positiva.

Derivando as duas funções temos:

Derivando novamente temos:

Passo 2

Pela primeira derivada vemos um ponto critico em , pois se igualarmos qualquer uma das duas a zero, encontraremos esse valor.

Passo 3

Pela cara da segunda derivada, conseguimos dizer com clareza que não existem pontos de inflexão e nem sermos capazes de calcular valores de máximo e mínimo mas isso não significa que não temos mudança de direção, e essa mudança ocorre sempre que o valor dentro de módulo for 0,pois é o limiar para a troca de sinal.

Fazendo a conta acharemos

Passo 4

Por se tratar de uma função de segundo grau simples dentro do módulo me absterei de fazer os limites para achar a assíntota horizontal pois não há nenhum impeditivo sem ser o de sinal. Então para valores extremos a função sempre será +

Fazendo então a tabela com os valores:

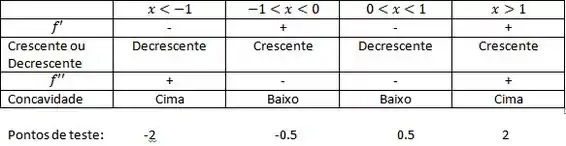
Para o crescimento por ter modulo maior que 1 os dois valores extremos pertencerão a segunda equação , e os dois do meio por ter módulo menor que 1 estarão fazendo parte da primeira equação.

Para a concavidade sempre que a função tiver módulo menor que 1 a derivada segunda será negativa(-2) e caso o módulo seja maior a derivada segunda será 2, o que será sempre positivo.