Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 43

Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

43-

y = 8 x x 2 + 4

Passo 1

Note que a função não tem assíntotas verticais pois não tem como o denominador ser menor que 0.

Fazendo a primeira derivada para essa função temos:

y ' = 8 x ' x 2 + 4 - ( 8 x ) ( x 2 + 4 ) ' x 2 + 4 2

y ' = 8 x 2 + 4 - ( 8 x ) ( 2 x ) x 2 + 4 2 ∴ - 8 x 2 + 32 x 2 + 4 2

Agora fazendo a derivada segunda dessa função temos:

y ' ' = - 8 x 2 + 32 ' x 2 + 4 2 - [ - 8 x 2 + 32 x 2 + 4 2 ' ] x 2 + 4 4

y ' ' = - 16 x x 2 + 4 2 - [ - 8 x 2 + 32 2 x 2 + 4 2 x ] x 2 + 4 4

y ' ' = x 2 + 4 [ - 16 x x 2 + 4 - [ - 8 x 2 + 32 4 x ] ] x 2 + 4 4

y ' ' = - 16 x 3 - 64 x + 32 x 3 - 128 x x 2 + 4 3

y ' ' = 16 x 3 - 192 x x 2 + 4 3 ∴ 16 x ( x 2 - 12 ) x 2 + 4 3

Passo 2

Analisando o numerador de y ' temos:

- 8 x 2 + 32 = 0

x = ± 2

Então temos como pontos críticos os valores de x iguais a +2 e -2.

Já o denominador teria valores imaginários de x , o que diz que não tem.

Passo 3

Agora temos que testar os valores que encontramos e se a função possui pontos de inflexão.

Para x = 2 temos:

y ' ' 2 = 16 × 2 ( 2 2 - 12 ) 2 2 + 4 3 = 32 × - 8 512 → n e g a t i v o

Logo para x = 2 temos máximo local, concavidade para baixo

Para x = - 2 temos:

y ' ' - 2 = 16 × - 2 ( ( - 2 ) 2 - 12 ) ( - 2 ) 2 + 4 3 = - 32 × - 8 512 → p o s i t i v o

Vendo agora os pontos de inflexão temos:

16 x × x 2 - 12 = 0

Para a expressão acima ser zero temos duas possibilidades:

16 x = 0

x 2 - 12 = 0

Então temos três pontos de inflexão:

x = 0 ;     x = ± 12      

Passo 4

Vendo agora se temos assíntotas horizontais:

lim x → ∞ ⁡ 8 x x 2 + 4 - L ' H o p i t a l ∞ ∞ - lim x → ∞ ⁡ 8 2 x = 0

lim x → - ∞ ⁡ 8 x x 2 + 4 - L ' H o p i t a l ∞ ∞ - lim x → - ∞ ⁡ 8 2 x = 0

Então a função tende a zero com valores extremos, logo a assíntota horizontal é 0.

Passo 5

Arrumando nossos intervalos:

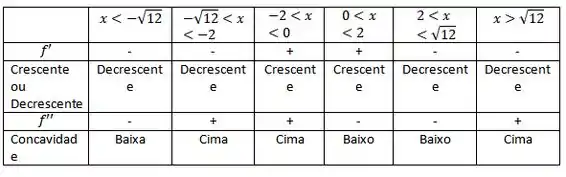
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item 5.9 . 3 . d) y = 2 x x + 2
Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item 5.9 . 3 . c) x 4 - 32 x + 48 .
Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item 5.9 . 3 . d) y = cosh ⁡ x
Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item 5.9 . 3 . d) y = 2 x 2 - 2 x - 3
Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item 5.9 . 3 . f x = x 4 - x 2