Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 14f
Olhando para o gráfico, estude a variação do sinal de .
Passo 1
Primeiro vamos começar pelo esboço dessa função. Ela é uma funçãod e segundo grau, portanto a cara dela é de uma parábola. Para esboçar uma parábola precisamos determinar quatro pontos principais: as duas raíses, o ponto onde a função corta o eixo e o vértice. Vamos lá?
Primeiro as raízes:
Usando a fórmula de Bhaskara com temos:
Assim os dois primeiros pontos (nosso caso aqui eles são iguais) são: .
Passo 2
Agora vamos pros outros dois? Bola lá! O ponto onde a função corta o eixo é onde :
Então o ponto no qual a função cruza o eixo é o .
Passo 3
Por último o vértice:
Assim temos o vértice . Como o coeficiente é menor do que zero, a parábola tem boca para baixo. E mais, o valor de é o maior que a função assume. Juntando os quatro pontos, podemos construir o gráfico:
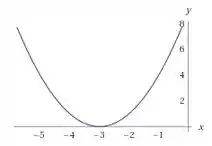
Beleza! Agora sim podemos analisar o sinal da função!
A função assume valores positivos quando está acima do eixo , e valores negativos quando está abaixo.
Sendo assim temos que nossa função assume apenas valores igual ou maiores do que zero:
Certo? Vamos pra próxima?