Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 24

Um papagaio (pipa) a 100 pés acima do solo move-se horizontalmente a uma velocidade de 8 pés/s. A que taxa está decrescendo o ângulo entre a linha e a horizontal depois de 200 pés de linha serem soltos?

Passo 1

Opa, bora lá! Vamos analisar o que nosso probleminha está falando.

Bom, ele nos diz que uma pipa tem a velocidade horizontal constante, e nos pede a velocidade que o ângulo entre a linha e a horizontal diminui cada vez que a pipa se afasta, sabendo que ela já está a 200 pés de distância.

Vamos fazer um esqueminha para entender o que está acontecendo.

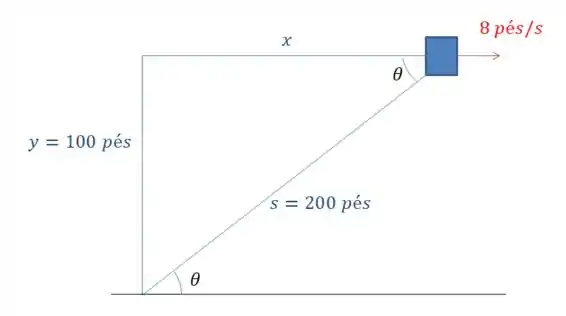
Repare que podemos dizer que o ângulo θ da linha com a horizontal é o mesmo ângulo que eu coloquei dentro do triângulo.

Nosso primeiro passo vai ser achar a relação com o ângulo.

Podemos dizer que:

t g θ = C O C A

Onde o cateto adjacente é a distância horizontal x e o cateto oposto é altura y que é constante e vale 100 pés.

t g θ = 100 x

Passo 2

Como queremos encontrar a variação do ângulo, vamos derivar a expressão final do passo 1 com relação ao tempo.

d d t t g θ = d d t   100 x - 1

sec 2 ⁡ θ d θ d t = 100 - 1 x - 2 d x d t

Organizando isso aí para d θ d t , temos:

d θ d t = - 100 x 2 1 sec 2 ⁡ θ d x d t

Agora, como sabemos que:

d x d t = 8 p é s / s

Podemos substituir e achar:

d θ d t = - 800 x 2 sec 2 ⁡ θ

Agora precisamos encontrar a posição x e a secante desse ângulo no instante dado.

Passo 3

Para encontrar a posição x , podemos usar Pitagóras.

s 2 = x 2 + y 2

Onde no instante dado, teremos:

200 2 = x 2 + 100 2

40000 = x 2 + 10000

x 2 = 30000

E para encontrar a secante do ângulo θ nesse instante, vamos lembrar que a secante é:

sec ⁡ θ = 1 c o s s e n o θ

sec ⁡ θ = H P C A

Que para o nosso ângulo, no instante dado, teremos:

sec ⁡ θ = s x

Como queremos a secante ao quadrado, faremos:

sec 2 ⁡ θ = s 2 x 2

sec 2 ⁡ θ = 40000 30000 = 4 3

Agora basta substituirmos tudo na expressão que encontramos no final do Passo 2.

d θ d t = - 800 30000   4 3

d θ d t = - 800 400000

Simplificando,

d θ d t = - 1 50 r a d / s

Prontinho!

Resposta

d θ d t = - 1 50 r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 Ache a função rendimento marginal;Ache o rendimento marginal quando x = 30.
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid
Se R(x) for o rendimento total recebido das vendas de x aparelhos de televisão e R x = 600 x - 1 20 x 3 c) Ache o rendimento real da venda da vigésima primeira televisão.
Uma frente fria aproxima-se de uma região. A temperatura é T graus t horas após a meia-noite e T = 0,1 400 - 40 t + t 20 ≤ t ≤ 4 Ache a taxa de variação média de T em relação a t entre 5h e 6h;