Uma partícula se move com
- Encontre a velocidade no instante
- Qual a velocidade depois de
- Quando a partícula está em repouso?
- Quando a partícula está se movendo no sentido positivo?
- Encontre a distância total percorrida durante os 8 primeiros segundos
- Desenhe um diagrama como na figura 2 para ilustrar o movimento da partícula
- Encontre a aceleração no instante e depois de
- Faça os gráficos das funções posição, velocidade e aceleração para
- Quando a partícula está acelerando? Quando está freando?
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função posição de uma partícula
E nosso objetivo é a partir dela encontrar uma série de coisas: A função velocidade, a velocidade em , quando a partícula está em repolso, quando o movimento da partícula é positivo, a distancia percorrida no intervalo de , encontrar a função aceleração, esboçar os gráficos da posição, velocidade e aceleração, encontrar a aceleração em e por fim determinar o intervalo de tempo quando a partícula está acelerando e quando a partícula está freiando.
É muita coisa, não é?
Bom... para resolver esse problema temos que lembrar dos princípios físicos que diz que a velocidade é a variação da posição sobre a variação no tempo
E a aceleração é a variação da velocidade sobre a variação do tempo.
Trazendo isso para a nossa realidade, taxa de variação é a mesma coisa que derivada em um função, ou seja
Então derivando a função vamos obter a função velocidade e derivando a função velocidade, vamos obter a função aceleração...
Veja só!
Passo 2
Se , então
Pela regra da potência
Show? A partir dessa função podemos responder os quatro primeiros quesitos do problema...
Veja só!
Passo 3
No item a) é pedido a velocidade em função do tempo .
Isso é justamente o que fizemos no passo 2, ou seja
No item b) é pedido a velocidade em , então substituímos em e encontramos o resultado.
No item c) temos que descobrir quando a partícula está em repouso...
Pensando fisicamente, se uma partícula está em repolso, significa que ela está parada, logo, sua velocidade é nula.
Isso acontece quando , ou seja
Nesse caso, não existe valores de que satisfazem essa igualdade, então a partícula nunca está em repouso.
Já no item d) queremos saber quando a partícula está se movendo no sentido positivo, ou seja, quando
Essa função é sempre positiva, então a partícula está se movendo no sentido positivo em todos os instantes.
Tranquilo até aqui?
Passo 4
No item e) queremos saber qual a distancia percorrida nos primeiros segundos...
Pra isso vamos usar a função e substituímos
Bora continuar!
Passo 5
No item f) queremos ilustrar um gráfico que represente o movimento da matricula...
Vimos que o movimento é positivo, então é crescente.
Em ,
Com isso já sabemos de duas informações importantes, agora vamos determinar mais alguns pontos da nossa curva...
Em .
Em .
Em .
Em
Com essas informações, podemos esboçar o diagrama como
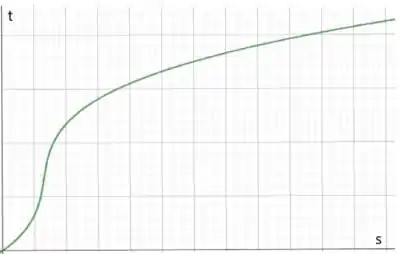
Bacana, não é?
Passo 6
No item g) queremos encontrar a função aceleração e a aceleração em .
Como vimos no passo 1.
Se , então
Pela regra da potência...
Substituindo , temos que a aceleração nesse instante é
Estamos quase no fim!
Passo 7
No item h), o problema pediu pra plotar os gráficos de , e usando uma ferramenta gráfica...
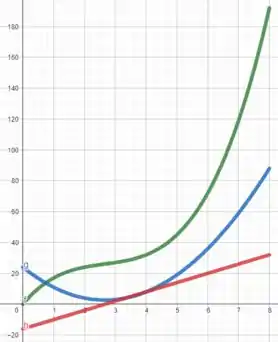
Em verde temos , em azul e em vermelho
Show de bola?
Passo 8
Por fim, no item i) queremos determinar os intervalos em que é positivo e negativo.
Se , será positivo se
A aceleração é positiva quando e é negativa quando .
É isso! O que achou? Responde Aí!
Resposta
a)
b)
c) não existe
d) todos os instantes
e)
f) 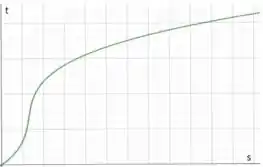
g) ,
h) 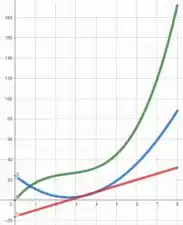
i)