Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 55
Na teoria da relatividade, a massa de uma partícula é
Em que é a massa de repouso da partícula, é a massa quando a partícula se move com velocidade em relação ao observador e é a velocidade da luz. Esboce o gráfico de como uma função .
Passo 1
Opa! Bora pra mais uma questão?!
O enunciado nos dá uma função que modela a massa de uma partícula, segundo a teoria da relatividade e pede pra a gente esboçar o seu gráfico:
Em que é a massa de repouso da partícula, é a massa quando a partícula se move com velocidade em relação ao observador e é a velocidade da luz.
Queremos desenhar o gráfico de como uma função .
Para isso podemos seguir o seguinte roteiro:
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
D. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
E. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
F. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
G. Esboçar a função juntando as informações obtidas.
Passo 2
Primeiramente iremos verificar o domínio de :
O denominador não pode ser igual a zero e a raiz não pode ser negativa, então:
Consideramos a partícula se movendo apenas em um sentido e a velocidade positiva.
Passo 3
Agora vamos falar de intersecção dos eixos! Para encontrarmos a intersecção com o eixo vertical, fazemos:
Não há interseção com o eixo horizontal .
O que implicaria em
No entanto é uma constante positiva maior do que zero.
Passo 4
Temos que verificar também a existência de assíntotas:
Para assíntotas horizontais temos que ter .
Sabemos que não pertence ao domínio da função, afinal
e terminamos de combinar no passo anterior que os valores negativos vão ficar de fora.
Dessa forma não temos assíntotas horizontais.
Para assíntotas verticais, vamos olhar o ponto de descontinuidade da função:
Como a raíz só assume valores positivos, temos:
Dessa forma, em temos uma assíntota vertical, a função explode para .
Passo 5
Para achar intervalos de crescimento e decrescimento precisamos calcular a derivada da nossa função:
Derivando, vamos aplicar a regra da cadeia e a regra da potência:
Resolvendo:
Para temos .
Então está crescendo em .
Não existem pontos de máximo nem mínimo locais.
Passo 6
Calculamos a segunda derivada pra descobrir a concavidade:
Derivando usando a regra da cadeia e a regra da potência novamente, teremos:
Resolvendo, temos:
Portanto:
Todos os termos dessa expressão são positivos para .
Como , então possui concavidade para cima em . Não existem pontos de inflexão na função.
Passo 7
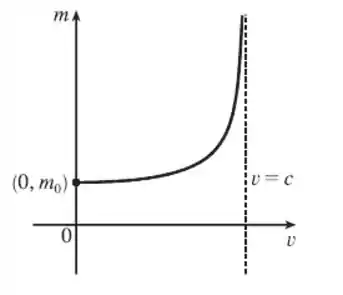
Agora sim, podemos desenhar o gráfico:
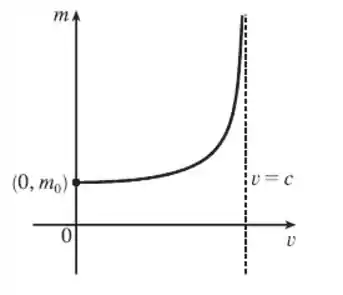
Resposta
