Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 58
A partir do Exercício 57, o polinômio tem um ponto de inflexão. Use um recurso gráfico computacional para tirar conclusões sobre o papel da constante na localização do ponto de inflexão. Use para explicar o que observou graficamente.
Passo 1
Então galera, de início vamos encontrar esse ponto de inflexão que o enunciado comentou, ok? Para fazermos isso temos que encontrar a derivada segunda da nossa função e igualar a zero, se liga:
Derivando pela primeira vez:
Pela segunda vez:
Ok, agora que derivamos vamos igualar a zero:
De fato a questão está certa, a função em questão só possui um ponto de inflexão, que é exatamente em .
Passo 2
Antes de analisarmos , vamos plotar o gráfico de :
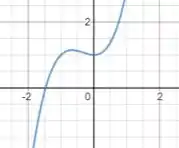
Neste gráfico fizemos . Quando alteramos o valor de o gráfico muda de comportamento, mas de duas maneiras: quando o ponto de inflexão é deslocado para a direita e quando o ponto de inflexão é deslocado para a esquerda. E essa é a nossa análise do problema, galera!
Resposta
Ei, a resposta está no passo a passo :)