Em cada parte, esboce o gráfico de uma função com as propriedades indicadas e discuta os sinais de e
(a) A função é côncava para cima e crescente no intervalo
Passo 1
Uma função côncava pra cima é uma função que possui uma “abertura” direcionada pra parte superior do eixo de coordenadas cartesianas. Logo, não pode ser uma função “em linha reta”, como uma função afim.
E uma função crescente é uma função cujos valores de correspondentes aos valores de selecionados, no intervalo avaliado, sempre aumentam, no sentido crescente do intervalo.
Juntando essas duas condições podemos pensar em alguns casos de funções que as atendam.
Passo 2
Um exemplo é . Observe:
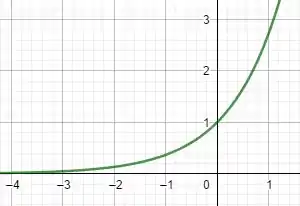
Passo 3
Temos:
e
Ambas sempre com sinal positivo, independentemente do valor de avaliado.
Resposta
Ei, a resposta está no passo a passo :)