46. a) Mostre que se .

b) Mostre que se .

c) Confirme as desigualdades de a) e b) com algum recurso gráfico computacional.

Para o primeiro caso:

Aplicando em ambos os membros da inequação, teremos:

Como , então:

Show de bola, agora para o segundo caso:

Aplicando em ambos os membros:

Sendo assim, de acordo com nossa derivada conseguimos concluir que, de fato, se .

b) Assim como na letra a), aqui temos o seguinte:

Para temos que o lado esquerdo da inequação da zero mesmo, então a igualdade não precisamos provar. No entanto, quanto à crescência teremos que utilizar o conceito de derivada primeira. A derivada primeira irá nos fornecer a prova necessária para demonstrar que, de fato, a função que escrevemos só é crescente quando . Sendo assim, derivando:

Agora o que devemos fazer é analisar os dois casos possíveis, que é para e para , então bora lá!

Para o primeiro caso:

Essa solução só é válida para . Já para o segundo caso:

Já para esse caso a solução só é válida para , como esperávamos! Sendo assim, de acordo com nossa derivada conseguimos concluir que, de fato, se .

c) Então galera, se plotarmos os gráficos das funções da letra a), ou seja:

Teremos:

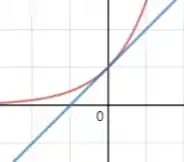
No qual a função em azul é e a função em vermelho é . Pelo gráfico conseguimos notar que para a função é maior do que .

Agora plotando os gráficos da letra b):

Teremos:

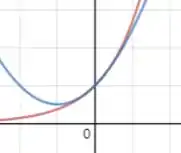
No qual a função em vermelho é e a função em azul é . Pelo gráfico também conseguimos notar que para a função é maior do que . Uma ressalva é que isso não ocorre para , como podemos notar.

E essa é a nossa análise da questão, pessoal!