O pedal de uma bicicleta é empurrado por um pé com força de , como mostrado. A haste do pedal tem de comprimento. Determine o módulo do torque em relação a .
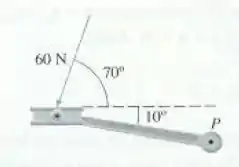
Passo 1
Fala aí! Partiu resolver essa questão de cálculo que parece física? haha Partiuuu!!
Bom, vamos lembrar que o módulo do torque é dado por essa equação aqui:
Nosso enunciado dá pra gente o módulo do vetor posição, que é o comprimento da haste do pedal, e a magnitude da força, além disso temos o ângulo entre eles que a imagem nos mostra… Então temos tudo! Mas precisamos de atenção na parte do ângulo, ok?
Na equação vamos usar o seno do ângulo formado entre a força e , beleza? Então vamos ter que:
Agora vamos fazer as continhas! Sem esquecer de ajustar a unidade do comprimento para metros, tranquilo? Teremos então:
ou
Prontinho! Conseguimos!