Calcule e determine se tem sentido de entrar ou sair da página.
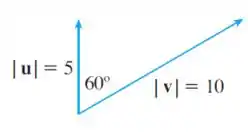
Passo 1
Devemos calcular o produto vetorial de dois vetores, onde é o ângulo entre e
Passo 2
Sabemos que qualquer vetor é ortogonal tanto à quanto à , temos que resulta em um vetor com direção perpendicular ao plano que passa por e . O sentido desse vetor é determinado pela regra da mão direita: com os dedos da mão direita curvados girando no sentido de para , seu polegar estará apontando na direção e sentido de . Com base nisso temos que o vetor entra na página.
Resposta
Entra na página