A figura mostra um vetor pertencente ao plano e um vetor na direção de Seus módulos são .
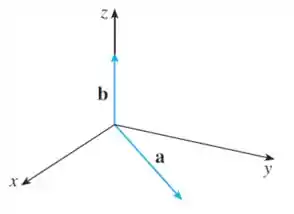
(a) Calcule
(b) Utilize a regra da mão direita para decidir se as componentes de são positivas, negativas ou nulas.
Passo 1
- Para calcularmos o módulo do produto vetorial basta usarmos a seguinte fórmula:
- Usando a regra da mão direita temos o vetor orientado conforme ilustrado na figura abaixo. Podemos ver que a componente do eixo está orientada no eixo positivo enquanto que no eixo está orientado no eixo negativo, o vetor não possui coordenada no eixo .
Passo 2
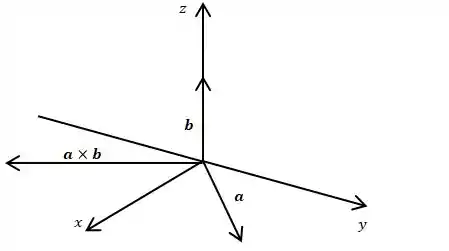
Resposta
Componente orientada positivamente
Componente orientada negativamente
Não possui componente em