Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 46

Para um peixe nadando a uma velocidade v em relação à água, a energia gasta por unidade de tempo é proporcional a v ³ . Acredita-se que os peixes migratórios tentam minimizar a energia total necessária para nadar a uma distância fixa. Se o peixe estiver nadando contra uma corrente u ( u < v ) , então o tempo necessário para nadar a uma distância L é L / ( v - u ) e a energia total E requerida para nadar a distância é dada por

E v = a v 3 L v - u

onde a é uma constante de proporcionalidade.

a) Determine o valor de v que minimiza E .

b) Esboce o gráfico de E

Observação: Esse resultado foi verificado experimentalmente; peixes migratórios nadam contra a corrente a uma velocidade 50 % maior que a velocidade corrente.

Passo 1

Fala aí, tudo certinho?

Bom, essa questão fala pra gente que a energia gasta por um peixe migratório ao nadar é dada pela expressão

E v = a v 3 L v - u

Sendo:

v a velocidade da correnteza;

L a distância que o peixe irá nadar;

u a velocidade do peixe;

a uma constante de proporcionalidade.

Queremos saber qual deve ser o valor de v que minimiza a energia E .

Para isso, usaremos a ideia de derivada, uma vez que quando a energia é mínima sua derivada vai a zero.

Então veremos isso acontecendo no passo a passo. Vem que te ajudo com isso.

Passo 2

Precisamos derivar E e igualar a zero para achar um possível valor mínimo. Sendo:

E v = a v 3 L v - u

a e L são constantes, beleza?! Utilizando a regra do quociente:

E ' v = 3 L a v 2 v - u - L a v 3 v - u 2

Fazendo as multiplicações, teremos:

E ' v = L a v 2 3 v - 3 u - v v - u 2

E ' v = L a v 2 2 v - 3 u v - u 2

Para termos E ' v = 0 fazemos:

2 v - 3 u = 0

v = 1,5 u

Lembrando que não poderíamos fazer v = 0 uma vez que v > u . Então, 1,5   u é a velocidade que minimiza E .

Ahh, no enunciado temos a seguinte observação “Esse resultado foi verificado experimentalmente; peixes migratórios nadam contra a corrente a uma velocidade 50 % maior que a velocidade corrente”.

Então o nosso resultado está certo! \o/

Passo 3

Agora temos que esboçar o gráfico. Para isso vamos analisar a função:

E v = a v 3 L v - u

Quando v tende a u E ( v ) tende a infinito, então teremos uma assíntota vertical. Sabemos que o gráfico não toca o eixo, pois a energia nem a velocidade pode ser igual a zero e além disso como v é sempre positivo e maior que u o nosso gráfico será sempre crescente.

Ahh, ali em cima calculamos o ponto mínimo também. Juntando todas essas informações chegamos em:

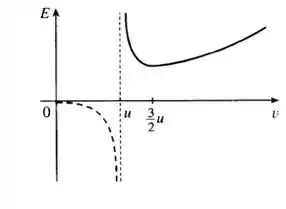
Resposta

  1. v = 1,5   u
  2. Gráfico acima.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um modelo usado para a produção Y de uma colheita agrícola como função do nível de nitrogênio N no solo (medido em unidades apropriadas) é Y = k N 1 + N 2 Em que k é um constante positiva. Que nível d
Uma empresa opera 16 poços de petróleo em uma área designada. Cada bomba, em média, extrai 240 barris de óleo diariamente. A empresa pode adicionar mais poços, mas cada poço adicionado reduz a produçã
Considere a reta tangente a elipse x 2 a 2 + y 2 b 2 = 1 no ponto ( p , q ) no primeiro quadrante.Mostre que a linha tangente intercepta x em a 2 / p e y em b 2 / q Mostre que a porção da reta tangent
Se o fazendeiro no Exercício 18 quiser englobar 150 metros quadrados de terra, que dimensões minimizarão o custo da cerca?
9. O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De