Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 5
5) Encontre a aproximação linear da função em e use-a para aproximar os números e . Ilustre fazendo os gráficas de e da reta tangente.
Passo 1
Fala aí! como vai? 😉
Nesse problema temos que encontrar a aproximação linear da função em e usar para aproximar os números e . Além disso temos que ilustrar fazendo os gráficas de e da reta tangente.
Parece complicado? 🤔
Para obter a linearização uma função , devemos utilizar a aproximação da função em :
Veja só! 😊
Passo 2
Para isso vamos derivar :
Então, em é:
Tranquilo até aqui? 👀
Passo 3
Agora, para , temos:
:
Já para , temos
:
Bacana, não é? 😉
Passo 4
Para ilustrar, temos o gráfico:
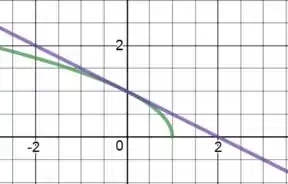
E aí! entendeu tudo? Responde Aí! 😬
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 7-14, determine uma linearização em um inteiro escolhido convenientemente próximo a x 0 em que a função dada e sua derivada sejam fáceis de calcular.13- f x = e - x, x 0 = - 0.1
Nos Exercícios 1-5, determine a linearização L(x) de f(x) em ( x - a ) .5- f x = t gx,a = π
Utilize a aproximação linear 1 + x k = 1 + k x para determinar uma aproximação para a função f(x) para valores de x próximos de zero.d) f x = 2 + x 2
Utilize a aproximação linear 1 + x k = 1 + k x para determinar uma aproximação para a função f ( x ) para valores de x próximos de zero.a) f x = 1 - x 6
Utilize a aproximação linear 1 + x k = 1 + k x para determinar uma aproximação para a função f ( x ) para valores de x próximos de zero.c) f x = 1 1 + x