Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 30
Uma pipa a acima do solo move-se horizontalmente a uma velocidade de . A que taxa descrece o ângulo entre a linha e a horizontal depois de de linha serem soltos?
Passo 1
Opa, bora resolver esse problema! Estamos soltando uma pipa e ela esta a do chão subindo horontalmente a uma velocidade de .
A nossa posição em relação a pipa é a seguinte:
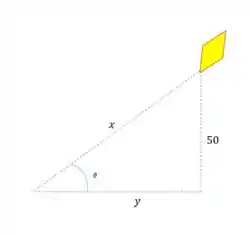
Seja , o ângulo descrito entre a linha e o chão, a distância horizontal que a pipa percorre e o comprimento da linha solta.
Queremos:
Depois de de linha serem soltos.
Passo 2
A relação entre e é:
Derivando em função do tempo em segundos, temos:
Passo 3
Quando metros de linha são soltos, então :
E é dado por:
Então, se temos:
Logo, o ângulo varia a uma taxa de rad/s.
Resposta
O ângulo varia a uma taxa de rad/s.
Exercícios de Livros Relacionados
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 Ache a função rendimento marginal;Ache o rendimento marginal quando x = 30.
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid
Se R(x) for o rendimento total recebido das vendas de x aparelhos de televisão e R x = 600 x - 1 20 x 3 c) Ache o rendimento real da venda da vigésima primeira televisão.