Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 18
Um holofote sobre o chão ilumina uma parede de m distante dele. Se um homem de m de altura anda do holofote em direção à parede a uma velocidade de m/s, quão rápido descreve o comprimento de sua sombra sobre a parede quando ele está a m dela?
Passo 1
Opa, bora resolver esse problema! Temos aqui um problema de taxa relacionada!
De um lado temos um holofote e do outro temos uma parede de que esta sendo iluminado pelo holofote. Um homem de de altura anda do holofote até a parede com uma velocidade igual a .
O que temos que responder é, qual a velocidade altura da sombra do homem na parede diminui?
Isso porque quando o homem esta no mesmo ponto que o holofote a sua sombra tem o tamanho da parede, que é , mas a medida que ele vai seguindo em frente essa sombra vai diminuir.
Vamos chamar a distância do homem ao holofote de e a distância do homem a parede de .
É importante lembrar que se a distância do holofote à parede é de m, então:
Queremos aqui achar:
Passo 2
A sombra do homem é projetada sobre a parede, descrevendo uma situação de semelhança de triângulos. Se chamarmos de , a altura da sombra, temos a seguinte situação:
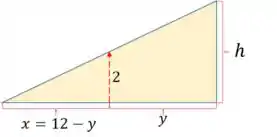
Logo, por semelhança de triângulos:
Passo 3
Logo, para achar a taxa com que varia, é só encontrar a sua derivada em função do tempo:
Quando e , e o homem caminha no sentido de crescimento de a uma taxa de m/s, então:
Logo, o comprimento da sombra decresce (por conta do sinal negativo) a uma razão de m/s.
Resposta
O comprimento da sombra decresce a uma razão de m/s.