Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 10
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada nas figuras a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Então expresse a força como uma integral e calcule-a.
Passo 1
A gente vai pegar essa figura bonitinha e fazer umas configurações doidas, saca só:
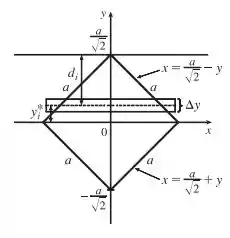
Pela metade de cima, o comprimento dessa faixa é , e sua área é .
A pressão nessa faixa é aproximadamente , então a força na faixa é aproximadamente .
Passo 2
A força total é
Passo 3
Pela metade inferior, o comprimento é e a força total é
Passo 4
Vemos que , assim, a força total é
Resposta
.
Exercícios de Livros Relacionados
9. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada nas figuras a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. E
Uma lâmina tem a forma de um triângulo retângulo de lados 3,4 e 5m. A lâmina está imersa verticalmente num líquido de tal forma que a hipotenusa coincide com o nível do líquido. Determinar a força exe
Nos exercícios 27 a 30 , temos uma comporta de uma represa, colocada verticalmente, com a forma indicada.Calcular a força total contra a comporta27.Um retângulo com 30m de largura e 10m de altura; nív
32. Uma chapa é limitada pela curva y = x 2 3 e a reta y = 1 , no plano x y , com o eixo dos y apontando para cima e suas escalas medidas em metros. A chapa está submersa em óleo, cujo peso 9.600N e w