Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 13
Uma vala é preenchida com um líquido de densidade . As extremidades da vala são triângulos equiláteros com lados de de comprimento e o vértice no fundo. Calcule a força hidrostática em uma extremidade da vala.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular a força hidrostática em uma extremidade de uma vala com líquido de densidade e sabendo que as extremidades dessa vala são triângulos equiláteros com de lado e vértice no fundo.
Esboçando esse triângulo, temos:
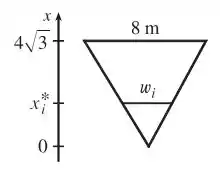
Onde é a largura da vala e a altura média do triângulo.
Pra calcular a força hidrostática na extremidade dessa vala, temos que lembrar que ela é dada pela integral do produto da área pela gravidade , densidade do fluido e altura :
A área nós conseguimos encontrar pelas relações de semelhança de triângulo, assim como a altura. Então, nós substituímos os dados fornecidos pelo enunciado e calculamos a integral.
Vamos lá!
Passo 2
Por semelhança de triângulos, a gente tem que:
A área da faixa retangular é e a pressão nela é , onde .
Passo 3
Assim, nossa força vai ser dada por:
Aplicando a distributiva nesse produto do integrando:
Integrando em relação a :
Aplicando os limites de integração, temos:
Mas sabemos que e . Então, substituindo, vamos obter:
Valeu, galera! Até a próxima! 😉