Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 50
- Avalie
Para
- Estime o valor de
- Calcule para valores sucessivamente menores de até finalmente atingir valor para . Você ainda está confiante que a conjectura em (b) está correta? Explique por que você acaba obtendo o valor .
- Faça o gráfico da função na janela retangular por . Dê então zoom na direção do ponto onde o gráfico corta o eixo para estimar o limite de quando tende a 0. Continue dando zoom até osbservar distorções o gráfico de . Compare com os resultados da parte (c).
Para
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos primeiramente calcular para os seguintes valores de :
e
Assim, basta substiruir na função que encontratemos o correspondente.
Depois, devemos estimar o valor do seguinte limite:
Para isso, resolveremos com base nos valores de encontrados na letra (a) pois, se você perceber, o tende cada vez mais a zero.
Em seguida, deveremos substituir na função mais uma vez, só que dessa vez iremos substituir por valores cada vez menores... até atingir o zero.
Por fim, vamos elaborar o gráfico da função na janela por e iremos aplicar sucessivos zooms a fim de observar o comportamento da função.
Agora bora lá!! 😉
Passo 2
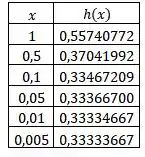
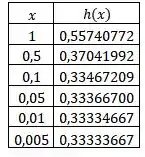
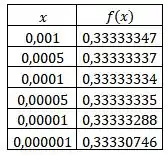
Primeiramente, construindo uma tabela para confrontar os valores de com ficamos com:
Passo 3
Pela tabela do item (a), percebemos que quanto mais se aproxima de zero, mais tende a , ou seja, mais tende a .
Matematicamente falando, podemos dizer que:
Passo 4
Agora, construindo outra tabela para confrontar os valores de (só que dessa vez ainda menores) com ficamos com:
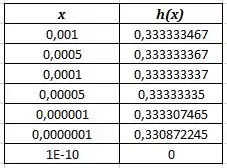
Note que os valores irão começar a variar ainda mais e saem do padrão de .
Passo 5
Fazendo o gráfico e dando sucessivos zoom’s, começando da janela por :
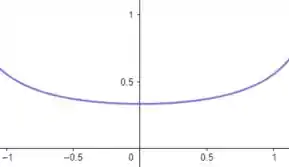
Agora, aplicando zoom, temos:
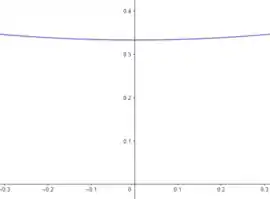
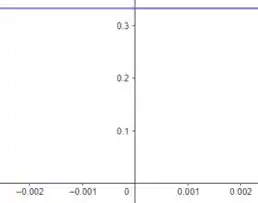
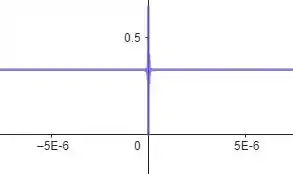
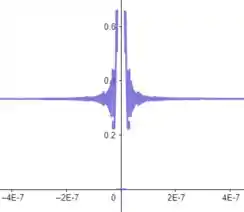
Podemos ver que o gráfico da função tem uma oscilação muito grande para valores de muito pequenos.
Resposta
-
-
- Podemos ver que o gráfico da função tem uma oscilação muito grande para valores de muito pequenos