Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.1 - Ex. 42

As curvas com equações x n + y n = 1 ,   n = 4 ,   6 ,   8 ,   … ,   são chamadas círculos gordos. Desenhe as curvas com n = 2 ,   4 ,   6 ,   8 e 10 para ver o porquê. Escreva uma integral para o comprimento L 2 k do círculo gordo com n = 2 k . Sem tentar calcular essa integral, determine o valor de lim k → ∞ ⁡ L 2 k .

Passo 1

Pensando pelo lado da simetria, o comprimento da curva em cada quadrante é o mesmo, então conseguimos esboçar o seguinte desenho:

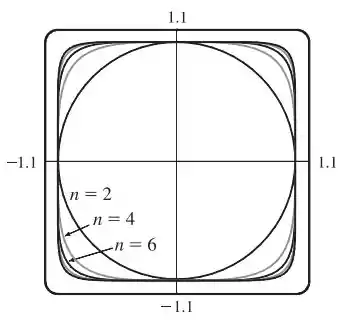
Assim, nós iremos calcular o comprimento do primeiro quadrante e multiplicar por 4 .

Passo 2

Então, pelo primeiro quadrante, temos que

x 2 k + y 2 k = 1 → y 2 k = 1 - x 2 k → y = 1 - x 2 k 1 2 k

Então, nós usamos a fórmula do comprimento de arco com

d y d x = 1 2 k 1 - x 2 k 1 2 k - 1 - 2 k x 2 k - 1 = - x 2 k - 1 1 - x 2 k 1 2 k - 1

Passo 3

Assim sendo, o comprimento total

L 2 k = 4 ∫ 0 1 1 + - x 2 k - 1 1 - x 2 k 1 2 k - 1 2 d x = 4 ∫ 0 1 1 + x 2 2 k - 1 1 - x 2 k 1 k - 2 d x

Agora, pelo gráfico, nós vemos que conforme k aumenta, os “cantos” dos círculos gordos ficam cada vez mais próximos de ( ± 1 , ± 1 ) , e ( ± 1 ,   ∓ 1 ) , e as “arestas” dos círculos gordos se aproximam das retas que unem esses quatro pontos. Parece plausível que conforme o comprimento total do círculo gordo com n = 2 k irá se aproximar do perímetro do quadrado de lados 2 .

Isso é comprovado fazendo o limite de k → ∞ da equação do círculo gordo do primeiro quadrante: lim k → ∞ ⁡ 1 - x 2 k 1 2 k = 1 para 0 ≤ x < 1 . Assim, nós supomos que : lim k → ∞ ⁡ L 2 k = 4 * 2 = 8 .

Resposta

8 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

28- Uso de segmentos tangentes para deduzir a fórmula de comprimento das curvas Suponha que f seja lisa em [ a , b ] e divida o intervalo [ a , b ] da maneira usual. Em cada subintervalo x k - 1 , x k
Use um sistema de computação algébrica ou uma tabela de integrais para achar o comprimento de arco exato da curva y = ln ⁡ x que está entre os pontos ( 1,0 ) e ( 2 , ln ⁡ 2 ) .
Use um sistema de computação algébrica ou uma tabela de integrais para achar o comprimento de arco exato da curva y = x 4 / 3 que está entre os pontos ( 0,0 ) e ( 1,1 ) .
Escreva uma integral para o comprimento da curva. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. x = y 2 - 2 y ,0 ≤ y ≤ 2
Encontre o comprimento exato da curva. y = x - x 2 + s e n - 1 x