Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 26
- Os planetas se movem ao redor do Sol em órbitas elípticas com o Sol em um dos focos. As posições de um planeta que estão mais próximas ou mais afastadas do Sol são chamadas respectivamente periélio e afélio do planeta. Use o Exercício para mostrar que a distância no periélio de um planeta até o Sol é e que sua distância no afélio é .
- Use os dados do Exercício para encontrar as distâncias da Terra até o Sol no periélio e no afélio.
Passo 1
Eaee, tudo certinho?? Bom... queremos demonstrar que a distância no periélio de um planeta até o Sol é e que sua distância no afélio é .
Mas o que é afélio e periélio??
Bom... são os pontos mais longo e mais próximo do Sol, respectivamente. Veja:
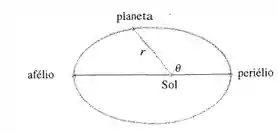
Para isso, vamos utilizar a equação que encontramos no exercício :
Onde é a excentricidade e é uma constante a distância entre o planeta e o Sol (que seria para aplicar para vários planetas).
Em seguida, devemos utilizar e para encontrarmos essas distâncias utilizando a Terra.
Passo 2
Bom... já vimos que:
Porém, o produto notável no numerador pode ser escrito da seguinte forma:
O que deixa a nossa cônica com essa outra cara:
Passo 3
E por ser uma elipse horizontal temos que os vértices maiores dessa elipse serão o afélio e o periélio com o periélio corresponde ao ângulo (o que deixa o denominador com o maior numero) e o afélio com o ângulo , logo o valor de no periélio será igual a:
Simplificando:
Agora a distância do afélio:
Simplificando:
Passo 4
A questão nos diz que:
E
Logo:
E