Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 14
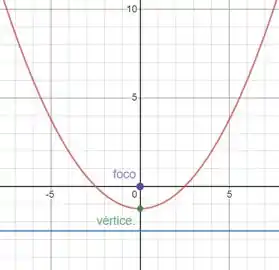
14- a) Encontre a excentricidade b) identifique a cônica c) dê uma equação da diretriz e d) esboce a cônica.
Passo 1
Eaee, belezinha? Bom... o enunciado nos deu a seguinte equação de uma cônica:
Primeiramente queremos encontrar a sua excentricidade . (Lembre-se que a excentricidade serve para nos dizer o quão "alongada" ou "achatada" é a forma da cônica.).
Para isso, vamos comparar a nossa equação com a seguinte equação geral:
Onde é a diretriz.
Com o valor da excentricidade, iremos identificar a cônica, onde:
- Se , trata-se de uma elipse;
- Se , trata-se de uma parábola;
- Se , trata-se de uma hipérbole.
Com a curva identificada, poderemos analisar e mostrar a equação da diretriz .
Por fim, iremos plotar a nossa curva. Agora bora lá!! 😉
Passo 2
Vamos adequar a questão do enunciado para bater com as equações encontradas no teorema :
Para isso vamos dividir numerador e denominador por :
Agora comparando as duas equações nós conseguimos dizer que a excentricidade dessa cônica vale:
Com a excentricidade valendo nós teremos uma parábola.
Passo 3
Pelo denominador ter uma função seno nós saberemos que a equação diretriz será uma reta em e pelo sinal dessa função ser negativo nós saberemos que é uma reta negativa de valor igual a:
Logo a equação da reta diretriz será:
Por ser uma reta na horizontal nós saberemos que a parábola será uma parábola vertical. Que terá um ponto de mínimo. E que se dará quando pois é quando .
Assim, terá um ponto de vértice igual a:
Se fizermos com encontraremos um ponto de vértice igual a:
O que faz sentido para uma parábola.
Passo 4
Gráfico da função:
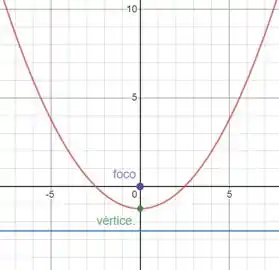
Onde a reta em azul é a diretriz.
Parâmetros:
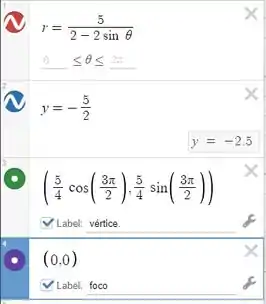
Resposta
