Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.5 - Ex. 12
Uma função é dada por uma tabela, gráfico, formula ou descrição verbal. Determine se a ela é injetora.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão diz pra gente que existem diferente maneiras de representar uma função, podendo ser através de uma tabela, de um gráfico, de uma fórmula ou de uma descrição verbal. Depois disso ela pede para que a gente diga de a função
É uma função injetora.
Primeiro, vamos ver o que é uma função injetora. De acordo com o livro, uma função injetra é aquela que nunca repete os valores de para diferentes, isto é:
sempre que
Então é isso que vamos analisar em nossa função. Vem comigo que te mostro como!
Passo 2
Agora sim, vamos para a função do enunciado.
Perceba que esta função é uma função ímpar, isto é,
Então não teremos valores simétricos de levando ao mesmo resultado em .
Além disso a função é uma raiz cúbica de , e o gráfico dessa função é do tipo:
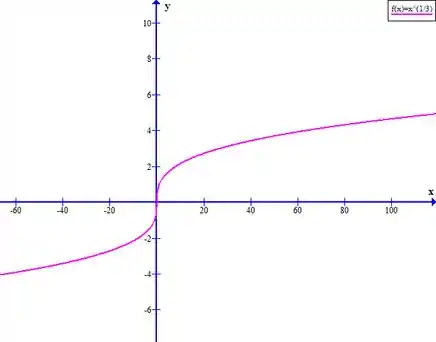
Bom, podemos perceber então que os valores nunca vão se repetir para qualquer .
Portanto, ela é uma função injetora.
Resposta
Sim,
É uma função injetora.