Um plano de telefone tem uma taxa de mensais. O plano inclui minutos gratuitos e taxa de 10 centavos para cada minuto adicional utilizado. Expresse o custo mensal C como uma função do número de minutos utilizados e esboce o gráfico C como uma função de para
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente escrever uma expressão para o custo mensal , de um plano de telefone, em função do número de minutos utilizados . Pra isso, ele nos disse que o plano tem uma taxa de mensais, que inclui minutos gratuitos e uma taxa de 10 centavos para cada minuto adicional utilizado. Além disso, nós devemos esboçar o gráfico dessa função, no intervalo
Então, vamos tentar traduzir essas informações em dados para a nossa função. Observe que, nesse plano, se você contratar o serviço, mesmo que você não use os minutos, você pagará uma taxa de Então, temos uma taxa fixa.
O plano ainda inclui minutos gratuitos e uma taxa de 10 centavos para cada minuto adicional utilizado. Então, esse valor depende do número de minutos utilizados .
Agora vamos tentar escrever uma expressão usando essas informações e plotar a função obtida no plano cartesiano.
Vamos lá!
Passo 2
Bom... Se você passar de minutos conversando com o crush, há uma cobrança de centavos por minuto a mais, ou seja, dos minutos que você usou é visto quanto passou de .
Em outras palavras, significa que é feito e o resultado multiplicado por . Então, considerando o custo fixo de , o nosso custo vai ter a seguinte cara, quando os minutos utilizados passarem de minutos:
E, se não passar de minutos, pagaremos apenas reais, ou seja:
Sendo assim, nossa função custo tem a seguinte cara:
Passo 3
Esboçando essa função, vamos ter:
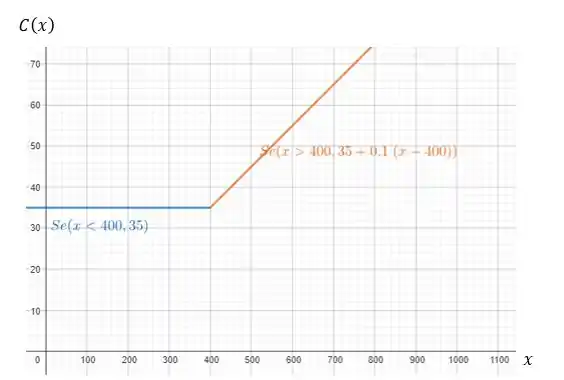
Valeu, galera! Até a próxima! 😉