Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.7 - Ex. 18
Plote o ponto cujas coordenadas esféricas são dadas. Depois, determine as coordenadas retangulares do ponto.
Passo 1
Para resolver esse exercício, vamos usar um software para plotar o ponto e após isso iremos usar as relações de transformação para coordenadas retangulares para descobrir as coordenadas nessa nova transformação.
Passo 2
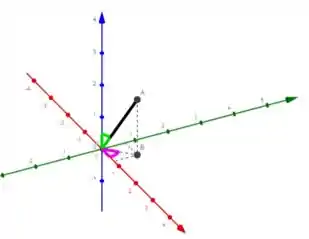
Passo 3
Para determinar iremos usar as relações para coordenadas cilíndricas
Temos que o raio é dado, uma vez que os pontos em coordenadas esféricas são dados por . Assim, temos que nosso , e serão
Resposta
Exercícios de Livros Relacionados
Encontre a equação cartesiana para a curva descrita pela equação polar dada.19. r = c o s s e cθ
Encontre a equação cartesiana para a curva descrita pela equação polar dada.15. r = 2
Encontre a equação cartesiana para a curva descrita pela equação polar dada.17. r = 3 sen θ
No exercício a seguir, ache a equação polar do gráfico, considerando a equação cartesiana dada. x 2 +y 2 - 9 x + 8 y = 0
No exercício a seguir, ache a equação cartesiana do gráfico tendo a equação polar dada. r 1 - c o s θ = 2