Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 34

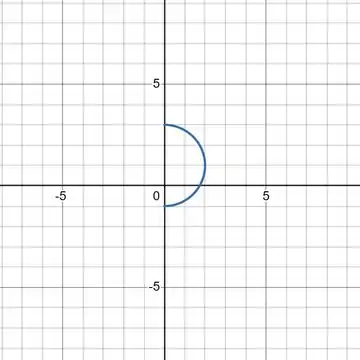
Plote o semicírculo traçado pela partícula no exercício 33(c).

Passo 1

Olá, meu amigo. Vamos resolver essa atividade.

A questão pede para plotarmos o semicírculo traçado pela partícula no exercício 33(c). Se voltarmos para o exercício 33, vemos que essa curva representa meia volta no sentido anti-horário, partindo do ponto .

A equação da circunferência é

Essa circunferência tem centro e raio .

Esta atividade é uma atividade que devemos utilizar um software gráfico, então eu estarei utilizando o Desmos.

Passo 2

Como a gente quer apenas a parte positiva, vamos reescrever nossa equação:

Iremos isolar o :

Aqui a gente tem só a parte positiva da circunferência:

Agora vamos plotar ela no nosso software:

Basta então colocar a equação na aba do lado esquerdo, que teremos a nossa figura.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Associe os gráficos das equações paramétricas x = f ( t ) y = g ( t ) Em a - ( d ) com as curvas paramétricas rotuladas de I - I V . Justifique.

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Encontre equações paramétricas para a elipse x 2 a 2 + y 2 b 2 = 1 Use as equações paramétricas para traçar a elipse quando a = 3 e b = 1 ,2 ,4e8 Como muda o formato da elipse quando b varia?

Mostre que as equações paramétricas x = x 1 + x 2 - x 1 t y = y 1 + y 2 - y 1 t Onde 0 ≤ t ≤ 1 descrevem o segmento de reta que une os pontos P 1 ( x 1 , y 1 ) e P 2 ( x 2 , y 2 ) .E encontre as equaç

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.