Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 27
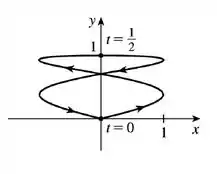
Use os gráficos de
Para esboçar a curva paramétrica
Indique com setas a direção na qual a curva é traçada à medida que aumenta.
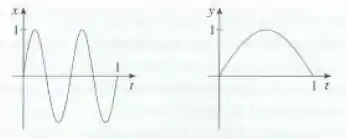
Passo 1
Olhando para os gráficos de e , dá pra ver de cara que quando, temos o ponto
Quando temos o ponto
Quando , temos o ponto
Então, podemos perceber que nosso gráfico começa da origem, depois ele vai pro ponto , que é o ponto mais alto da curva, e depois ele volta pra origem. Só que nesse meio tempo aí rola uns paranauê meio doido, porque repara só: quando o vai do para , o simplesmente cresce de para , mas o faz várias paradas. Ele cresce de zero pra um, depois decresce de zero pra , depois cresce de novo pra zero, pra só aí parar e chegar no ponto .
Aí quando o vai de para rola uma parada dessas de novo pra só então tudo voltar pro ponto .
Então quer dizer, parece que tem uma parada cíclica aí na nossa curva né.
Passo 2
Vamos agora tentar ver uns outros valores para e com isso achar mais ou menos uns outros pontos , plotar esses pontos e aí sim ver a cara que nossa curva toma.
Olhando de novo nossos gráficos:
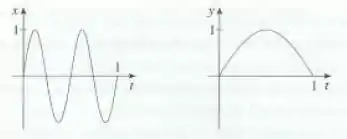
Se pegarmos , temos mais ou menos o ponto
Agora :
Vamos pegar agora :
Acho que já tá bom né?
Vamos plotar esses pontos. Vou numerar também a ordem em que a curva tem que passar em cada ponto de acordo com o valor de . Depois a gente liga tudo.
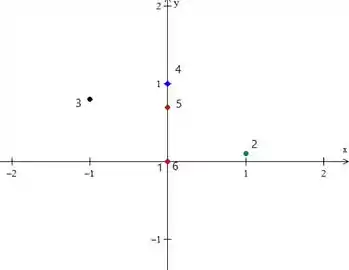
Agora se a gente ligar todos eles, teremos uma curva mais ou menos assim:
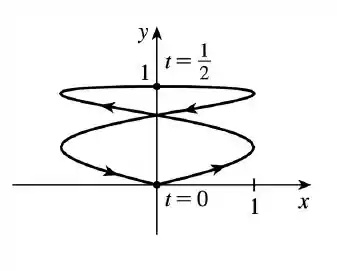
Resposta
