Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 34
- Encontre equações paramétricas para a elipse
- Use as equações paramétricas para traçar a elipse quando e
- Como muda o formato da elipse quando varia?
Passo 1
Fala ai pessoal. Boraresolver mais uma questão?
Primeira coisa que devemos fazer para parametrizar a equação da elipse, é utilizar as equações paramétricas e a relação fundamental trigonométrica.
Olha pra equação da elipse:
Repara que é uma soma de termos ao quadrado que é igual a 1.
Isso lembra bastante uma outra equação que também é assim. Essa daqui óh:
Então, parece uma boa igualar essas coisas que estão ao quadrado:
Isolando o e o , vamos ter
Pensando do mesmo jeito que a circunferência, teremos
Pronto! Encontramos as equanções paramétricas para a elipse do problema
Passo 2
Para a Letra b vamos usar as equações paramétricas que achamos, para traçar, com o auxílio de um programa gráfico, as elipses com fixo igual a e com os valores variados que a questão pede.
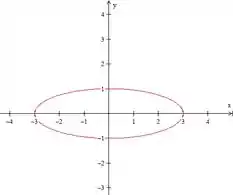
Para e :
Na horizontal o raio será 3
Na vertical o raio será 1
Plotando isso:
Passo 3
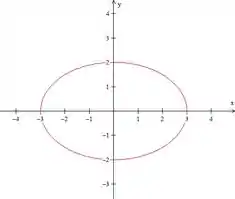
Para e :
Na horizontal o raio será 3
Na vertical o raio será 2
Plotando isso:
Passo 4
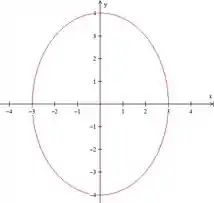
Para e :
Na horizontal o raio será 3
Na vertical o raio será 4
Plotando isso:
Passo 5
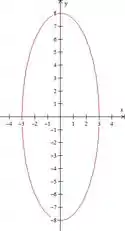
Para e :
Na horizontal o raio será 3
Na vertical o raio será 8
Plotando isso:
Passo 6
Na letra C conforme foi aumentando o valor de o que aconteceu foi que a elipse foi ficando mais achatada no eixo , pois o representa o tamanho do semieixo vertical da elipse.
Resposta
a)
b) Gráficos
c) conforme foi aumentando o valor de o que aconteceu foi que a elipse foi ficando mais achatada no eixo , pois o representa o tamanho do semieixo vertical da elipse.