Como podemos reconhecer se um problema pode ser resolvido utilizando o Teorema de Pappus? Ou seja, quais são as “pistas” e as “incógnitas” que poderiam sugerir uma tal solução? Discuta dois ou três exemplos.

Um exemplo onde o volume de um sólido de rotação foi pedido no exercício onde a gente precisava achar o volume de um toro elíptico.

A gente tinha a equação da elipse, daí a gente tirava a distância do centroide até o eixo de rotação. E sabíamos que a área da elipse era:

Era só jogar na fórmula e achar o volume.

O segundo caso que a gente pode discutir é o exercício onde precisávamos achar o centroide de um semicírculo de raio , sabendo que o volume da esfera é:

Nós olhamos esse problema pensando como a esfera poderia ser obtida girando o semicírculo em torno de um eixo, o eixo . Nesse caso, tínhamos o volume e a conseguíamos a área do semicírculo:

E , na real, era a própria coordenada que faltava do centroide, a . Olha na figura:

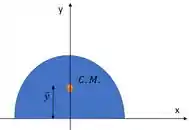
Nossa equação ficava assim:

Era só substituir tudo e isolar .