Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 37

A polia e os aparelhos de um guindaste são suspensos em um armazém por duas cordas de comprimento de 2 m e 3 m. O guindaste pesa 350 N. As cordas, amarradas em diferentes alturas, formam ângulos de 50° e 38° com a horizontal. Encontre a tensão em cada corda e a magnitude de cada tensão.

Passo 1

Faremos com que e sejam os vetores tensão correspondentes aos cabos de suporte conforme a figura a seguir:

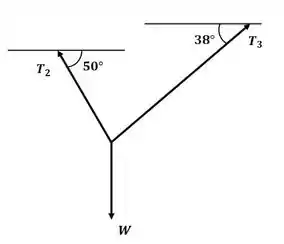
Com isso, podemos escrever e em termos de suas componentes vertical e horizontal:

Passo 2

Sendo assim, temos que a resultante das tensões, , logo:

Igualando as componentes em , temos:

Agora igualando as componentes em :

Substituindo a relação encontrada para as magnitudes nessa última equação, obtemos:

E, substituindo esse valor na relação obtida para as magnitudes de tensão, obtemos:

Passo 3

Dessa forma, os vetores tensão são dados por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um varal de roupas é estendido entre dois postes, 8 m distantes um do outro O fio do varal está bastante esticado, de forma a ser considerado horizontal. Quando uma camisa molhada com massa de 0,8 kg

Encontre o módulo da força resultante e o ângulo que ela faz com o eixo x positivo.29.

Cordas de 3 m e 5 m de comprimento são atadas à decoração natalina suspensa sobre uma praça. A decoração tem massa de 5 kg. As cordas, atadas em diferentes alturas, fazem ângulos de 52 ° e 40 ° com a

Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção N 45 ° W a uma velocidade de 50 km/h.

Se r =x , y , z e r 0 =x 0 , y 0 , z 0 , descreva o conjunto de todos os pontos ( x , y , z ) tal que r - r 0 = 1