Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.2 - Ex. 37

Um varal de roupas é estendido entre dois postes, 8 m distantes um do outro O fio do varal está bastante esticado, de forma a ser considerado horizontal. Quando uma camisa molhada com massa de 0,8 kg é pendurada no meio do varal, esse ponto central é deslocado para baixo em 8 cm. Determine a tensão em cada metade do varal.

Passo 1

Nessa questão temos mais uma situação em que precisamos interpretar o enunciado e encontrar um vetor resultante, vamos ilustrar melhor o que está acontecendo no varal:

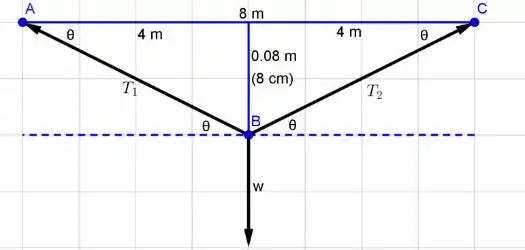
Como o sistema está em equilíbrio, sabemos que a somatória das componentes em x e em y é igual a 0 .

Primeiro note que w = 0,8   9,8 = 7,84 N é o peso da camisa.

Também precisamos da informação sobre o ângulo θ . Podemos encontrar ele fazendo

θ = tan - 1 ⁡ 0,08 4 ≈ 1,15 °

Beleza! então agora vamos montar nosso sistema.

- | t 1 | cos ⁡ 1,15 ° +   | t 2 | cos ⁡ 1,15 ° = 0 (1)

t 1 s e n   1,15 ° + t 2 s e n   1,15 ° = 7,84 (2)

Isolando t 2 na equação (1), ficamos com:

t 2 = t 1

Podemos substituir isso em (2):

t 1 s e n   1,15 ° + t 1 s e n   1,15 ° = 7,84

2 t 1 s e n   1,15 ° = 7,84

t 1 = | t 2 | ≈ 196

Esses são os módulos de cada tensão em cada metade do varal, agora vamos encontrar os vetores dessas tensões.

t 1 = ( - | t 1 | cos ⁡ θ i + | t 1 | s e n   θ ° j ) ≈   - 196 i + 3,92 j  

t 2 = | t 2 | cos ⁡ θ ° i + t 2 s e n θ ° j ≈ 196 i + 3,92 j

Então os vetores das tensões em cada fio são:   t 1 ⁡ ≈   - 196 i + 3,92 j   e   t 2 ≈ 196 i + 3,92 j

Resposta

33. t 1 = | t 2 | ≈ 196

t 1 ⁡ ≈   - 196 i + 3,92 j   e   t 2 ≈ 196 i + 3,92 j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam a → e b → nao-nulos.(b) Obtenha a expressão para p r o j u → p r o j v → p r o j u → v → .
Sejam a → e b → nao-nulos.(a) Enuncie uma condição necessária e suficiente para que a projeção ortogonal de a → sobre b → seja igual à projeção ortogonal de b → sobre a → .
No paralelogramo ACBD, os lados AB e AD medem, respectivamente, 3 e 9, e o ângulo interno de vértice A mede 60°. Sejam M o ponto DC e N o ponto AD tais que D M → = 3 M C → e 3 A N → = 2 A D → . Calcul
A norma de A X → , sendo X o ponto de interseção de A MeB N .
(a) Prove que u → + v → + w → 2 = u → 2 + v → 2 + w → 2 + 2 u → ∙ v → + u → ∙ w → + v → ∙ w → , quaisquer que sejam u → , v → e w → .(b) Dados os vetores não-nulos u → , v → e w → , sejam α = a n g u