Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção NW a uma velocidade de km/h. (Isso significa que a direção da qual está ventando está a a oeste da direção norte.) Um piloto está virando seu avião na direção NE a uma velocidade relativa (velocidade em ar parado) de km/h. O curso verdadeiro ou trajetória do avião é a direção da resultante dos vetores velocidades do avião e do vento. A velocidade escalar em relação oo solo do avião é o módulo da resultante. Determine o curso real e a velocidade escalar em relação ao solo do avião.

Nessa questão nós temos um baita enunciado contando uma historinha sobre aviões que exemplifica uma aplicação para vetores, mas de forma simplificada, o que nós queremos é calcular o vetor resultante da soma de outros dois, seu módulo e direção.

Então vamos desenhar os vetores que a questão nos deu para ficar mais fácil de entender:

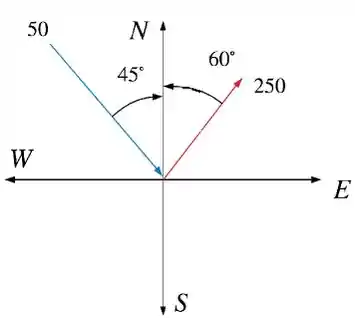
Para encontrar o vetor resultante, nós precisaremos decompor os dois vetores, somar suas componentes e então calcular o módulo do vetor resultante.

Vamos chamar de o vetor do vento, com módulo igual 5 km/h. Decompondo ele temos:

Substituindo os valores:

Agora vamos decompor o vetor que representa o avião:

Para encontrarmos o vetor resultante , basta somarmos as componentes de e , assim: