O ponto está sobre a curva .
- Se é o ponto use sua calculadora para determinar a inclinação da reta secante , com precisão de seis casas decimais, para os seguintes valores de
(i)0 (ii) 0,4 (iii)0,49 (iv) 0,499
(v) 1 (vi) 0,6 (vii) 0,51 (viii) 0,501
(b) Usando os resultados da parte (a), estime o valor da inclinação da reta tangente à curva no ponto
(c) Usando a inclinação da parte (b), encontre uma equação da reta tangente à curva em
(d) Esboce a curva, duas das retas secantes e a reta tangente.
Passo 1
Eaeee, belezinha?? Bom... a questão nos diz que um ponto está sobre a curva
O item (a) pede a inclinação da reta secante , pra diferentes pontos , que assume os oito valores de dados:
(i)0 (ii) 0,4 (iii)0,49 (iv) 0,499
(v) 1 (vi) 0,6 (vii) 0,51 (viii) 0,501
Bom, a inclinação de uma reta (também chamada de coeficiente angular) é a diferença da variável sobre a diferença da variável :
Na notação aqui na nossa questão, considerando os pontos e da reta secante :
No item (b), vamos usar o resultado encontrado pra estimar o valor da inclinação da reta tangente à curva no ponto Pra isso, temos que perceber que os valores de nos oito pontos calculados, se aproximam de 0,5 por cima e por baixo.
No item (c), a questão quer que calculemos uma equação da reta tangente à curva em . Então a gente vai precisar lembrar da fórmula geral da reta (função de primeiro grau), que tem o coeficiente angular e o coeficiente linear :
Como vamos usar a inclinação (coef. angular) encontrada no item anterior, é só achar o .
E por fim, a questão quer um gráfico, mas isso a gente discute quando chegar la!
Então bora lá!! 😉
Passo 2
Primeiro vamos calcular os valores de dos pontos de pra cada dado, basta substituir cada valor na fórmula dada do ponto.
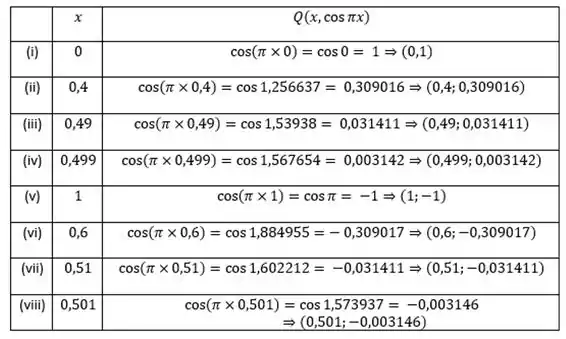
Feito isso, calculamos a inclinação da reta secante , com cada ponto calculado:
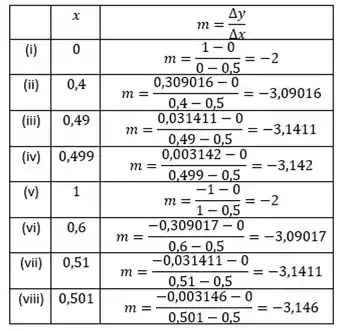
Passo 3
No item (b) queremos a inclinação da reta tangente num outro ponto, diferente dos que calculamos anteriormente, que o ponto
Pra fazer isso, vamos olhar bem pra tabela que que calculamos no item anterior, dividindo ela em valores maiores que 0,5 e valores menores que 0,5:
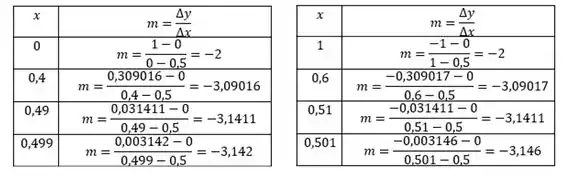
Repara que os valores de estão se aproximando de 0,5. E ao mesmo tempo, os valor também parece convergir pra um mesmo número.
Para calcular nosso resultado, o que nós vamos fazer é a média das inclinações das duas retas secantes mais próximas, que no caso são:
Parece sensato pensar que a nossa resposta vai ta no meio desses valores ne?
Então a inclinação em vai ser:
Passo 4
Bom, agora queremos a equação dessa reta tangente no ponto
Mas considerando que já achamos o coeficiente angular
A equação da reta vai ficar
Agora é moleza! É só achar o coeficiente linear. E pra isso só precisamos de um ponto e ele pode ser o próprio ponto . Substituindo na reta:
Então a equação da reta tangente NESTE PONTO vai ser:
Ufa! Agora só falta o gráfico.
Passo 5
Agora vamos traçar o gráfico da curva, de duas das retas secantes e da reta tangente. Mas a gente ainda não calculou as equações das retas secantes. No item (a), a gente calculou apenas as inclinações. Mas relaxa que é fácil. A gente vai fazer a mesma coisa que fez no item (c), só que pra outras 2 retas.
Mas primeiro vamos escolher 2 das secantes que vimos anteriormente (podem ser quaisquer duas):

Já temos os coeficientes angulares das 2, agora é só fazer que nem no item (c), substituir um ponto na equação da reta e calcular o coeficiente linear . Lembrando que todas essas retas passam pelo ponto , então podemos usar sempre ele.
Pra primeira reta secante, que passa por temos , então a reta vai ser:
No ponto :
Pra segunda reta secante, que passa por temos , então a reta vai ser:
No ponto :
Ufa! Bora pro gráfico!
Passo 6
Relembrando as funções que temos que traçar:
CURVA
RETA TANGENTE
RETAS SECANTES
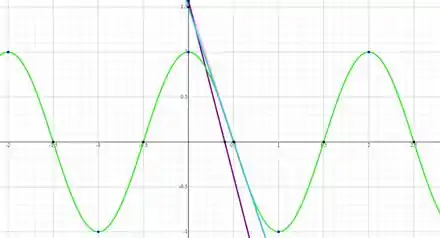
Pra esboçar retas, basta pegar 2 pontos da reta, colocar no plano cartesiano e ligá-los. Já temos todos os dados necessários. Mas vou trazer um gráfico da Calculadora gráfica do Symbolab.
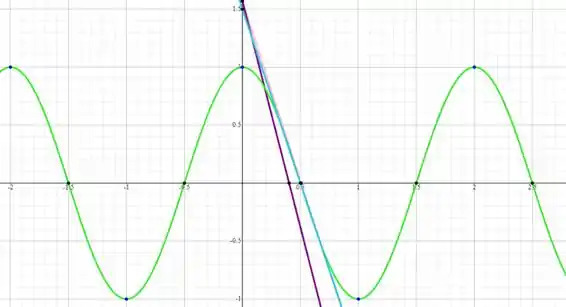
A curva está em verde
A reta tangente em rosa
A reta azul é a secante
E a reta roxa é a secante
Pode reparar que a reta azul se aproxima muito da reta rosa. Isso acontece porque ela foi calculada com pontos e muito próximos. Ela quase parece uma tangente (parece mas não é).
Já a reta roxa, foi calculadas com pontos bem distantes, então ela já fica bem diferente no gráfico.
Resposta
a) 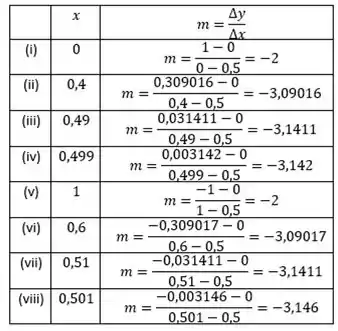
b) -3,144
c)
d)