Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 11
Esboce o gráfico da função e use-o para determinar os valores de para os quais existe:
Passo 1
Falaaaaaa aí, belezinha?? Bom... a questão nos dá a seguinte função :
Com isso, a questão nos pede para esboçar o gráfico de e utilizá-lo para determinar os valores de para os quais existe.
Nesse sentido, vamos entender cada parte da função para esboçar o gráfico.
Em seguida, vamos aplicar os limites laterais para determinar o valor de .
E aí?? Bora lá??!! 😉
Passo 2
Primeiro vamos montar um gráfico para cada parte:
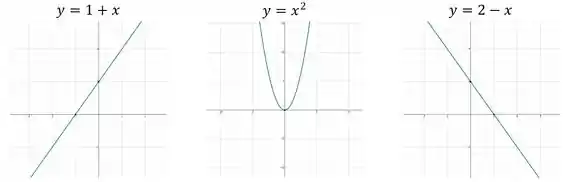
Show de bola, agora vamos aplicar as condições:
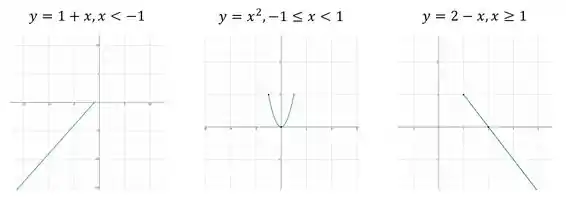
E, unindo os gráficos com auxílio de uma calculadora gráfica, temos:
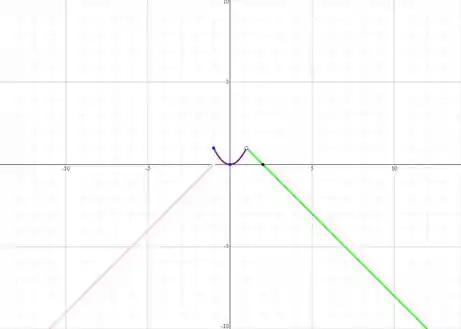
Passo 3
Show de bola. Olhando de novo pra nossa , vemos que ela é definida por partes em intervalos bem determinadinhos:
E saca só, em cada intervalo, a lei de formação também é muito bem definida! E definida por polinômios diferentes!
Bem, polinômios não são funções com pegadinhas.
Pra qualquer polinômio de qualquer ordem, vale:
E logo, o limite existe.
Ok mas perai, então não existe nenhum em que o limite de não exista?
Calma gafanhoto, nossa função não é um polinômio e sim uma função definida por partes com cada parte sendo um polinômio. No ponto em que a lei de formação muda, pode dar ruim.
Vamos testar então!
Passo 4
Para temos:
Então o limite em não existe galera, já que os limites laterais são diferentes.
Poderíamos resolver também pra olhando pro gráfico que montamos e vendo que em as funções não se conectam.
Pra agora, temos:
Opa, os limites aqui são iguais! Então só mesmo em que o limite não existe! Feshow
Resposta
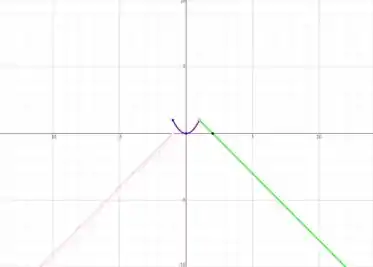
Existe para todo