Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 60

Em qual ponto sobre a curva y = 1 + 2 e x - 3 x   a reta tangente é paralela à reta 3 x - y = 5 ? Ilustre fazendo o gráfico da curva e de ambas as retas.

Passo 1

Opa, vamos fazer essa questão! O enunciado nos dá:

y = 1 + 2 e x - 3 x

3 x - y = 5

Vamos dizer que:

y 1 = 1 + 2 e x - 3 x

y 2 = 3 x - 5

Temos que achar um ponto onde a reta tangente de y 1 é paralela à y 2 . Sabemos que a derivada de uma função em determinado ponto é igual a inclinação da reta tangente nesse ponto, certo?!

Agora, o que precisa pra duas retas serem paralelas?!

Elas precisam ter o mesmo coeficiente angular! Logo para que a reta tangente de y 1 seja paralela a y 2 ela deve ter coeficiente angular igual a 3 ! A equação de uma reta pode ser dada por:

y - y 0 = m x - x 0

Onde m é o coeficiente angular e ( x 0 ,   y 0 ) é um ponto que pertence a reta. Conhecemos m e agora precisamos ir atrás das coordenadas!

Passo 2

Vamos derivar y 1 :

y 1 = 1 + 2 e x - 3 x

Vamos usar a regra da potência:

f x = x n

f ' x = n x n - 1

Além disso temos a função exponencial natural:

f x = e x

f ' x = e x

Derivando:

y 1 ' = 2 e x - 3 x

Queremos que y 1 ' = 3 :

2 e x - 3 = 3

2 e x = 6

e x = 3

Temos que:

e b = a ↔ ln ⁡ a = b

Portanto:

x = ln ⁡ 3

Agora vamos calcular f ( ln ⁡ 3 ) :

f ln ⁡ 3 = 1 + 2 e ln ⁡ 3 - 3 ln ⁡ 3

f ln ⁡ 3 = 1 + 2 3 - 3 ln ⁡ 3

f ln ⁡ 3 = 7 - 3 ln ⁡ 3

Passo 3

Finalmente podemos calcular a equação da reta:

y - y 0 = m x - x 0

Substituindo:

y - ( 7 - 3 ln ⁡ 3 ) = 3 ( x - ln ⁡ 3 )

y = 3 x - 3 ln ⁡ 3 + 7 - 3 ln ⁡ 3

y = 3 x - 6 ln ⁡ 3 + 7

Passo 4

Pra acabar precisamos do esboço dos gráficos:

y 1 = 1 + 2 e x - 3 x

y 2 = 3 x - 5

y = 3 x - 6 ln ⁡ 3 + 7

Plotando:

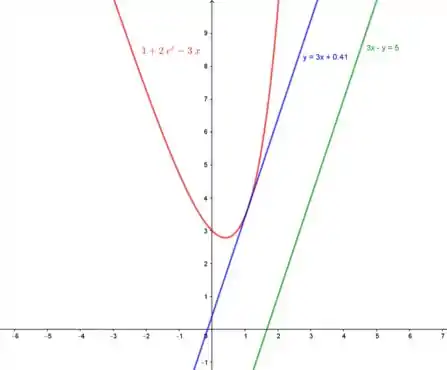
Prontinho!!

Resposta

y = 3 x - 6 ln ⁡ 3 + 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as equações para as retas que sejam tangente e normais à curva no ponto dado. x + x y = 6 4,1
Encontre as equações para as retas que sejam tangente e normais à curva no ponto dado. x 3 2 + 2 y 3 2 = 17 1 , 4
Encontre as equações para as retas que sejam tangentes e normais à curva no ponto dado. x 2 + 2 y 2 = 9 , ( 1 ,2 )
Determine os pontos na curva y=2 x 3 - 3 x 2 - 12 x + 20 em que a tangente seja paralela ao eixo x .
Determine os pontos na curva y = 2 x 3 - 3 x 2 - 12 x + 20 em que a tangente seja a. perpendicular à reta y = 1 - x 24 .b. paralela à reta y = 2 - 1 2 x .