Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 56

Que valores de x   fazem com que o gráfico de f x = e x - 2 x   tenha uma reta tangente horizontal?

Passo 1

Opa, vamos fazer essa questão! O enunciado nos da:

f x = e x - 2 x

E pergunta em quais valores de x temos uma tangente horizontal nessa curva!

Bom, para que uma reta seja horizontal, seu coeficiente angular tem que ser zero, certo?! Quem é o coeficiente angular da reta tangente em uma curva? A derivada né?!

Então o que a gente tem que fazer é descobrir os valores no qual a derivada de f ( x ) é zero!

Passo 2

Vamos derivar:

f x = e x - 2 x

Vamos usar a regra da potência:

f x = x n

f ' x = n x n - 1

Além disso temos a função exponencial natural:

f x = e x

f ' x = e x

Derivando:

f ' x = e x - 2

Agora igualamos a zero:

e x - 2 = 0

e x = 2

Colocando o l n dos dois lados:

ln ⁡ e x = ln ⁡ 2

Temos que:

ln ⁡ a = b ↔ e b = a

Portanto:

ln ⁡ e x = x

Assim:

x = ln ⁡ 2

Então quando x = ln ⁡ 2   temos uma reta tangente horizontal! A questão já esta respondida, mas podemos plotar o gráfico pra conferir:

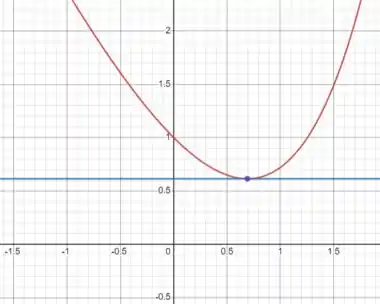
Prontinho!

Resposta

x = ln ⁡ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre f ' ( x ) . Verifique se sua resposta é razoável comparando os gráficos de f e f ' . f x = a r c t g ( x 2 - x )
Encontre uma equação da reta tangente à curva no ponto dado. y = x 3 - 3 x + 1 , ( 2,3 )
Se a equação de uma reta tangente à curva f ( x ) em 4,3 passar pelo ponto 0,2 encontre f 4ef ' ( 4 ) .
Encontre uma equação da reta tangente à curva no ponto dado. y = 4 x - 3 x 2 ,( 2 , - 4 )
Encontre uma equação da reta tangente à curva no ponto dado. y = 2 x + 1 x + 2 , ( 1,1 )