Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 55

Sejam a e b números positivos. Ache o comprimento do menor segmento de reta que é cortado pelo primeiro quadrante e passa pelo ponto ( a , b ) .

Passo 1

Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??

“Hulk esmaga”, Bora esmagar essa questãozinha comigo?

A questão pede para encontrar o comprimento do menor segmento de reta que cruza o primeiro quadrante e passa pelo ponto a ,   b , onde ( a )   e   ( b )   são números positivos.

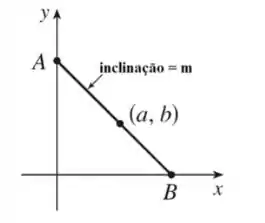
O primeiro quadrante é a região do plano cartesiano onde tanto ( x ) quanto ( y )   são positivos. Queremos encontrar a menor reta que atravessa essa região e passa pelo ponto ( a ,   b ) .

Passo 2

Para resolver essa questão, precisamos utilizar algumas propriedades das retas e da geometria analítica:

Equação da Reta: A equação de uma reta que passa por um ponto x 1 ,   y 1 e tem um coeficiente angular ( m ) é dada por:

      y   -   y 1 =   m x   -   x 1

Substituindo o ponto a , b :

      y   -   b   =   m x   -   a

Interceptos com os eixos:

- O intercepto com o eixo ( x ) ocorre quando ( y   =   0 ) :

          0   -   b   =   m x   -   a

x   =   a   - b m

- O intercepto com o eixo ( y ) ocorre quando ( x   =   0 ) :

          y   -   b   =   m 0   -   a

y   =   b   -   m a

Comprimento do Segmento de Reta:

- O comprimento do segmento de reta entre os pontos

x 1 ,   y 1   e   x 2 ,   y 2

é dado pela fórmula da distância entre dois pontos:

d = x 2 - x 1 2 + y 2 - y 1 2

Passo 3

Queremos encontrar os interceptos da reta com os eixos ( x )   e   ( y ) e calcular o comprimento desse segmento de reta.

Para minimizar esse comprimento, podemos ajustar o coeficiente angular ( m ) .

Dado o ponto a ,   b , substituímos na fórmula da equação da reta para encontrar os interceptos com os eixos ( x )   e   ( y ) .  

Calculamos os interceptos:

- Intercepto com o eixo ( x ) : a - b m ,   0

- Intercepto com o eixo ( y ) : 0 ,   b - m a

Depois, usamos a fórmula da distância para calcular o comprimento do segmento de reta entre esses dois pontos.

Passo 4

Encontrar os interceptos

Intercepto com o eixo x :

x = a - b m

a - b m , 0

Intercepto com o eixo y :

y = b - m a

= ( 0 ,   b - m a )

O comprimento ( L ) do segmento de reta é:

L = 0 - a - b m 2 + b - m a - 0 2  

Para facilitar a resolução, vamos usar S m = d 2 , assim some essa raiz chata!

S m = a - b m 2 + a m - b 2

S m = a 2 - 2 a b m + b 2 m 2 + a 2 m 2 + b ²

Passo 5

Finalmente minimizando essa coisa enorme:

S ' m = 2 a b m 2 - 2 b 2 m 3 + 2 a 2 m - 2 a b

S ' m = 2 m 3 ( a b m - b 2 + a 2 m 4 - a b m 3

S ' m = 2 m 3 b a m - b + a m 3 a m - b

S ' m = 2 m 3 a m - b b + a m 3

Igualando S ' ( m ) a zero:

m = b a       �� o u         m = - b a 3

Como b / a é maior que zero e m precisa ser menor que zero, m = - b a 3 .

Passo 6

Agora para fechar com chave de ouro, vamos encontrar S - b a 3 :

S - b a 3 = a + b a b 3 2 + - a b a 3 - b 2

= a + a b 2 3 2 + a 2 b 3 + b 2

S - b a 3 = a 2 + 2 a 4 3 b 2 3 + a 2 3 b 4 3 + a 4 3 b 2 3 + 2 a 2 3 b 4 3 + b 2

= a 2 + 3 a 4 3 b 2 3 + 3 a 2 3 b 4 3 + b 2

A última expressão está na forma

x 3 + 3 x 2 y + 3 x y 2 + y 3 = x + y 3

Com

x = a 2 3         e         y = b 2 3

então a gente pode escrever isso como a 2 3 + b 2 3 3 , então o menor seguimento mede

d 2 = S = a 2 3 + b 2 3 3

d = a 2 3 + b 2 3 3 2

“OK, isso foi legal.”

Resposta

d = a 2 3 + b 2 3 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função erro, denotada por fer, é definida por f e r x = 2 π ∫ 0 x e - t 2 d t Ache um valor aproximado da f e r ( 1 ) para quatro casas decimais, usando a regra de Simpson com n = 10 .
Para a função densidade de probabilidade normal padrão determine a probabilidade de que uma escolha ao acaso de x esteja no intervalo [ 0 ,1 ] . Aproxime o valor da integral definida usandoA regra de
Para a função densidade de probabilidade normal padrão determine a probabilidade de que uma escolha ao acaso de x esteja no intervalo [ 0 ,1 ] . Aproxime o valor da integral definida usandoA regra do
Para a função erro definida no Exercício 29, ache um valor aproximado para fer(10) até quatro casas decimais, usando a regra de Simpson com n = 10.
Para a função densidade de probabilidade normal padrão, determine a probabilidade de que uma escolha ao acaso de x esteja no intervalo [ - 3 ,3 ] . Aproxime o valor da integral definida usandoA regra