Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 64
A água escoa pelo fundo de um tanque de armazenamento a uma taxa de litros por minuto, onde . Encontre a quantidade de água que escoa do tanque durante os primeiros dez minutos.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que a água escoa pelo fundo de um tanque de armazenamento a uma taxa (em litros/minuto) dada pela seguinte função:
Onde .
Queremos encontrar a quantidade de água que escoa do tanque durante os primeiros dez minutos.
Tenha em mente que sempre que o enunciado te der uma taxa ele está falando da derivada, então o problema nos deu a derivada e quer o total de água que escoa nos 10 primeiros minutos, ou seja, a integral dessa função!
Então temos que integrar , para os primeiros dez minutos logo os limites de integração de a , ou seja:
Para facilitar nossa vida, podemos trabalhar com a tabela de primitivas:
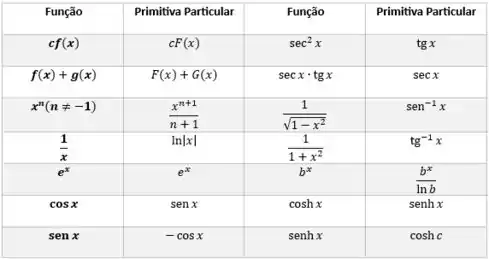
E aí avaliamos os limites da integração de acordo com o TFC (teorema fundamental do cálculo) que nada mais é que a primitiva no limite superior menos a primitiva no limite inferior:
E com isso vamos conseguir resolver nosso problema!
Prontos?
Passo 2
Então vamos resolver a integral:
Separando as duas:
Agora é só aplicar as regras que vimos no passo 1, vamos resolver elas separadamente, assim fica mais simples de ver:
Passo 3
Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Aplicando os limites:
Prontinho, temos a nossa resposta!
A quantidade de água que escoa do tanque durante os primeiros dez minutos é de litros.
Resposta
A quantidade de água que escoa do tanque durante os primeiros dez minutos é de litros.