Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 135

Fazer o gráfico da função

f x = s e n   x s e n   x

no intervalo 0   ,   3 π . Depois, analisar o observado.

Passo 1

É preciso saber o domínio da função.

D f = R

Passo 2

Encontrar a primeira derivada da função:

f ' x = s e n   x s e n   x 1 s e n   x ∙ c o s   x   s e n x   +   c o s   x ∙ ln ⁡ s e n   x

= c o s   x s e n   x s e n   x 1 + ln ⁡ s e n   x

Passo 3

Encontrar a segunda derivada da função:

f ' ' x = - s e n   x s e n   x - 1 1 + ln ⁡ s e n   x + c o s   x 2 s e n   x s e n   x 1 + ln ⁡ s e n   x 2 + c o s   x s e n   x s e n   x ∙ 1 s e n   x ∙ c o s   x =

= - s e n   x s e n   x - 1 1 + ln ⁡ s e n   x + c o s   x 2 s e n   x s e n   x 1 + ln ⁡ s e n   x 2 + c o s   x s e n   x s e n   x ∙ t g   x

Passo 4

Como se trata de uma questão que permite o uso da tecnologia, podemos utilizar o programa Wolfram Alpha para plotar o gráfico, tendo em vista o complexo trabalho algébrico encontrado através do método anterior.

Passo 5

Logo, temos:

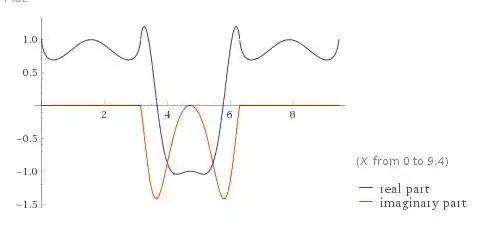
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se segunda a lei do movimento s = f ( t ) , t ≥ 0 , em que t é medido em segundos e s em metrosEncontre a velocidade no instante t Qual a velocidade depois de 3 s Quando a partícula
Use o roteiro dessa seção para esboçar a curva. y = x 3 + x
Use o roteiro dessa seção para esboçar a curva. y = x 3 + 6 x 2 + 9 x
Use o roteiro dessa seção para esboçar a curva. y = 2 - 15 x + 9 x 2 - x 3
Use o roteiro dessa seção para esboçar a curva. y = 8 x 2 - x 4