Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 44
Se
- Em quais pontos, se houver, o gráfico de tem um máximo local,um mínimo local ou um ponto de inflexão?
- Esboce a forma geral do gráfico.
Passo 1
Inicialmente considere em seguida identificaremos se possui pontos críticos para isso faremos, ou seja,
Aplicando a fórmula de Bhaskara obteremos que as raízes desse polinômio são e
Sendo assim temos dois candidatos à pontos críticos, vamos verificar se qual a mudança de sinal nas proximidades de cada um deles.
Perceba que, para valores dentro do intervalo , assume valores positivos (cresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, é um ponto de máximo no intervalo de
Já, para valores dentro do intervalo , assume valores negativos (decresce). E para valores dentro do intervalo , irá assumir valores positivos (cresce). Logo, é um ponto de mínimo no intervalo de
Passo 2
Determinaremos agora . Dessa forma , pela regra da diferença temos que
Passo 3
Como já determinamos podemos verificar se ela possui pontos inflexão, para isso faremos , ou seja,
Sendo assim temos um candidato a ponto de inflexão, vamos verificar se há mudança de sinal nas proximidades de cada um deles.
Perceba que, para valores dentro do intervalo , assume valores negativos (tem concavidade para baixo). E para valores dentro do intervalo , irá assumir valores positivos ( tem concavidade para cima). Logo, é um ponto de inflexão no intervalo de ou seja, possui uma mudança de concavidade nesse ponto.
Passo 4
Desejamos encontrar a foma geral do gráfico, porém, no enunciado só foi dado informações sobre a derivada de ou seja, .
Precisamos encontrar uma forma de voltar a função original, e quem vai nos ajudar com isso será a integral, pois por definição a integral é um anti-derivada. Sendo assim,
A constante está sendo levada em consideração pois estamos com uma integral indefinida, porém como desejamos em sua forma original consideraremos . Sendo assim,
Passo 5
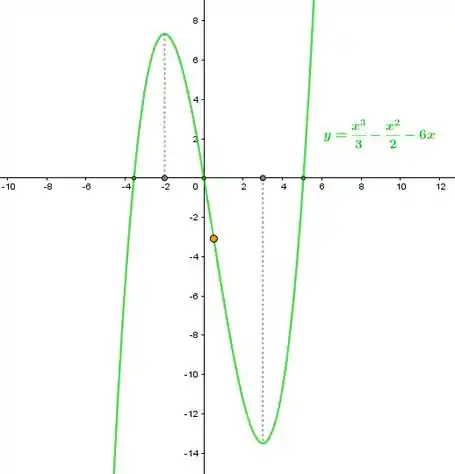Cuja forma geral do gráfico é,
Onde,
O ponto laranja corresponde ao ponto de inflexão
Os pontinhos verdes correspondem as raízes de
Os pontos cinzas correspondem aos pontos de mínimo () e de máximo ().
Resposta
Item a.
possui um máximo local em , um mínimo local em e uma mudança de concavidade em
Item b.
