Suponha que , em que e são polinômios sem fator comum. Se for uma assíntota horizontal do gráfico de , então e terão o mesmo grau.

Bom galera, essa afirmativa é verdadeira, agora vamos entender o porquê. Se o grau de for maior que o grau de , temos que é ilimitada em . No entanto, se o grau de for menor que o grau de , temos que quando .

Portanto, como é a assíntota, temos mais ou menos o seguinte:

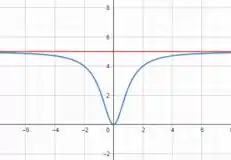
Assim, e terão o mesmo grau.

Prontinho!!