Quais pontos no plano satisfazem as equações e desigualdades nos Exercícios 11-16? Desenhe uma figura para cada exercício.
Passo 1
Olá pessoal, sabemos que as seções cônicas resultam da intersecção de um cone plano, como mostrado na Figura:
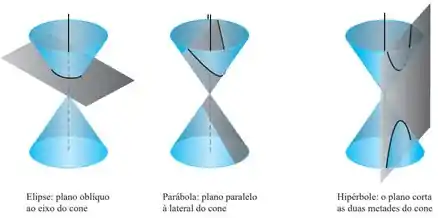
Equações de forma padrão para elipses centradas na origem:
- Distância entre o centro e foco:
- Focos:
- Vértices:
- Se concavidade para baixo;
- Se concavidade para cima.
- Distância entre o centro e foco:
- Focos:
- Vértices:
- Assíntotas: ou
Uma equação da parábola com foco e diretriz é:
Se considerarmos que , então a equação torna-se:
Equações de forma padrão para hipérbole centradas na origem:
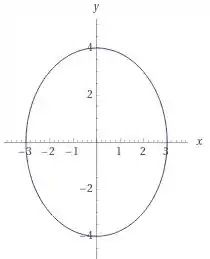
Sabendo disso, a equação:
É uma elipse com vértice e , então temos a figura:
Passo 2
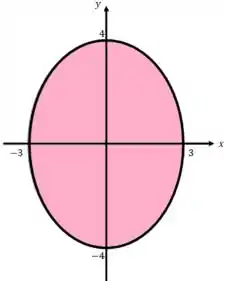
Então para:
Temos a seguinte região:
Tchau galerinha, estou te esperando no próximo exercício, até lá!
Resposta
Resposta no Passo.