Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 69
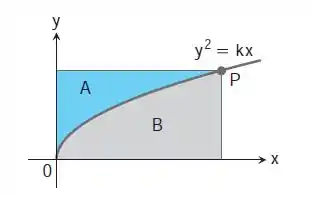
Se retas são traçadas paralelas aos eixos coordenados passando por um ponto P na parábola a parábola divide a região retangular delimitada por essas retas e os eixos coordenados em duas regiões menores, A e B.
a. Se as duas regiões menores são giradas em torno do eixo y, mostre que elas geram sólidos cujos volumes têm a razão 4:1.
b. Qual é a razão dos volumes gerados pelo giro das regiões em torno do eixo x?
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Pro item a), temos que:
Dessa forma,
Então o volume do solido gerado pela rotação da área, é dado por:
Portanto, temos a razão de 4 para 1 dentro da área.
Passo 2
Para o item b), calcularemos a razão dos volumes gerados pelo giro das regiões em torno do eixo x. Dessa forma,
Analogamente,
Então a razão para eixo x é de