Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.3 - Ex. 24

População regional: Se ƒ ( x ,   y )   =   100   ( y   +   1 ) representa a densidade populacional de uma região plana na Terra, onde x e y são medidos em milhas, encontre o número de pessoas na região delimitada pelas curvas x   =   y 2   e   x   =   2 y   –   y 2 .

Passo 1

Faaaala, cara! Tranquileba?

Primeiro, precisamos definir os limites de integral. Para isso, façamos o gráfico das funções dadas:

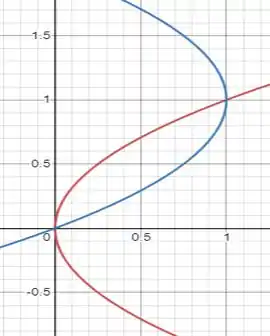
Onde pelos pontos onde as curvas se interceptam temos que 0 ≤ y ≤ 1 . E tendo que x dado em função de y, temos y 2 ≤ x ≤ 2 y - y 2 . Assim:

∫ 0 1 ∫ y 2 2 y - y 2 100 ( y + 1 ) d x   d y

Passo 2

100 ∫ 0 1 y + 1 x y 2 2 y - y 2   d y

100 ∫ 0 1 y + 1 2 y - 2 y 2 d y

200 ∫ 0 1 ( y + 1 ) ( y - y 2 ) d y

Passo 3

200 ∫ 0 1 y 2 - y 3 + y - y 2 d y

200 ∫ 0 1 y - y 3 d y

200 1 2 y 2 - 1 4 y 4

200 1 2 - 1 4

200 1 4

50

Resposta

50

Exercícios de Livros Relacionados

Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = e - x , y = 1 e x
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = tg ⁡ x , x = 0 e
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = x 2 e y = x + 2 .
Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 0 π ∫ 0 x x sen ⁡ y d yd x
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = x , y = 0 e x = 9