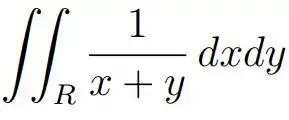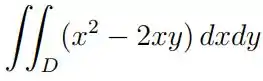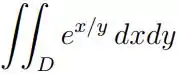Exercícios de Integrais Duplas sobre Regiões Gerais - Lista de Exercícios Resolvida
Questão 2
Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total sabendo que é a região triangular de vértices e a densidade em cada ponto é igual à distância de ao eixo
Ver solução completaQuestão 4
Determine o esboço da região do plano sobre a qual a integral é calculada:
Ver solução completaQuestão 6
Seja .
a) Esboce hachurando a região e ao lado a fronteira de .
b) Seja a integral dupla
Escreva na forma iterada, integrando primeiro em relação a e em seguida em relação a .
c) Escreva na forma da soma de duas integrais, integrando primeiro em relação a e depois a .
d) Agora, considere a integral dupla
em que . Calcule pelo método que preferir.
Ver solução completaQuestão 16
Considere a região plana definida por
Sejam uma função contínua definida em , e .
a) Esboce e, ao lado, esboce o interior de (ou seja, o conjunto aberto obtido removendo-se de a sua fronteira).
b) Escreva a integral dupla na forma de uma integral iterada, integrando primeiro com respeito a e depois com respeito a .
Ver solução completaQuestão 18
Calcule as seguintes integrais duplas:
d)
Onde é a região limitada por .
Ver solução completaQuestão 19
Calcule onde e é a parte da esfera no primeiro octante, com orientação para fora.
Ver solução completaQuestão 21
Use integral dupla para calcular a área da região limitada por:
No primeiro quadrante.
Ver solução completaQuestão 22
Encontre a área da região limitada pela parábola e pela reta utilizando integral dupla:
Questão 23
Considere uma lâmina que ocupa a região planar que se encontra entre a reta e a parábola . Suponha que a densidade em um ponto qualquer na lâmina seja dada pela função . Determine a massa total da lâmina.
Ver solução completaQuestão 24
- Calcule a integral dupla da função sobre a região triangular de vértices .
- A integral acima expressa o volume de qual sólido?
Ver solução completaQuestão 25
Considere uma lâmina que ocupa a região planar que se encontra entre as curvas , e . Suponha que a densidade em um ponto qualquer na lâmina seja dada pela função . Determine a massa total da lâmina.
Ver solução completaQuestão 26
A massa do conjunto
e
cuja densidade superficial é
é igual a
Escolha uma:
a)
b)
c)
d)
e)
Ver solução completaQuestão 27
Seja
- Seja uma função contínua definida na região . Escreva a integral dupla
- Escreva a integral dupla do item obrigatoriamente como uma integral iterada, integrando primeiro com respeito a e em seguida com respeito a .
- Calcule
Obrigatoriamente na forma de uma integral iterada, integrando primeiro com respeito a e em seguida com respeito a .
Obs.: Obviamente, nos itens e não é pedido cálculo de integral.
Questão 29
Quarta Questão: Calcule a integral.
onde é a região triangular com vértices , .
Ver solução completaQuestão 31
Questão 1: Considere as regiões do plano
Seja .
d) Considere a integral dupla
Escreva na forma de uma integral iterada, integrando primeiro com respeito a e em seguida em relação a .
Escreva na forma de uma diferença de integrais simples:
Explicitando , , e .
Obs.: Neste item não é necessário encontrar o valor numérico da , apenas escrevê-la no formato pedido.
e) Escreva na forma de uma soma de integrais iteradas, integrando primeiro com respeito a e em seguida com respeito a .
Obs.: Neste item não é necessário calcular as integrais.
Ver solução completaQuestão 32
Encontre a área da região limitada pela parábola e pela reta utilizando integral dupla:
Questão 33
Responda os itens a seguir.
(a) Sejam e funções integráveis em uma região limitada do plano. Se para todo qual a relação entre e ?
(Obs: não precisa justificar a relação)
(b) Use a relação do item (a) para mostrar que
onde é a região delimitada pelas retas
Ver solução completaQuestão 34
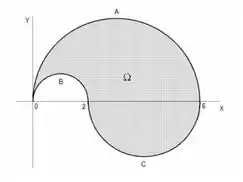
Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
1. vendo como domínio de tipo 1
Questão 35
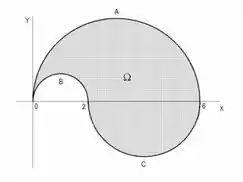
Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
2. vendo como domínio de tipo 2
Questão 37
Considere a integral
Onde é a região do primeiro quadrante limitada pelas retas , , e .
Escreva a integral em coordenadas sobre o domínio colocando os domínios de integração explícitos. (Não precisa resolver a integral).
Ver solução completaQuestão 38
- Calcule a integral abaixo
Ondeé o triangulo do plano cartesiano cujos vértices são , e .
Ver solução completaQuestão 39
Calcule
, onde é a porção limitada do primeiro quadrante que está entre as duas hipérboles e as duas retas .
Ver solução completaQuestão 45
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
a)
Ver solução completaQuestão 46
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
d)
Ver solução completaQuestão 48
2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis definida numa região é dada pela fórmula
Se é dada implicitamente pela equação , então
onde e supondo que nesse caso no interior de . Determine a área das seguintes superfícies:
c) A parte da esfera que está dentro do paraboloide .
Ver solução completaQuestão 50
2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis definida numa região é dada pela fórmula
Se é dada implicitamente pela equação , então
onde e supondo que nesse caso no interior de . Determine a área das seguintes superfícies:
a) A parte do plano que está no primeiro octante.
Ver solução completaQuestão 51
2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis definida numa região é dada pela fórmula
Se é dada implicitamente pela equação , então
onde e supondo que nesse caso no interior de . Determine a área das seguintes superfícies:
b) A parte da superficie que está dentro do cilindro .
Ver solução completaQuestão 53
(Cap 15.1 – Ex 12) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Ver solução completaQuestão 56
(Cap 15.3 – Ex 25) Determine o volume do sólido dado.
Abaixo da superfície e acima do triângulo com vértices , e
Ver solução completaQuestão 57
(Cap 15.1 – Ex 11) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Ver solução completaQuestão 58
(Cap 15.3 – Ex 31) Determine o volume do sólido dado.
Limitado pelo cilindro e pelos planos , , no primeiro octante.
Ver solução completaQuestão 59
(Cap 15.3 – Ex 13) Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.
D é limitada pelas retas , , .
Ver solução completaQuestão 60
(Cap 15.3 – Ex 14) Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.
D é limitada pelas retas ,
Ver solução completaQuestão 61
(Cap 15.3 – Ex 21) Calcule a integral dupla.
é limitada pelo círculo de centro na origem e raio
Ver solução completaQuestão 62
(Cap 15.3 – Ex 22) Calcule a integral dupla.
é a região triangular com vértices e .
Ver solução completaQuestão 63
(Cap 15.3 – Ex 11b) Desenhe um exemplo de uma região que seja
- Do tipo I, mas não do tipo II
- Do tipo II, mas não do tipo I
Questão 75
- Calcule a integral abaixo
Ondeé o triangulo do plano cartesiano cujos vértices são , e .
Ver solução completaQuestão 78
Seja uma função contínua em , tal que para todo pertencente a . Considere as seguintes afirmações:
A(s) afirmação(ões) verdadeira(s) para toda função como acima é(são):
Ver solução completaQuestão 79
12 - Calcule , onde é a região triangular limitada pela reta e os eixos coordenados.
Ver solução completaQuestão 81
Se é um triângulo de vértices (0,0), (2,0) e (0,2) então o valor da integral é:
Ver solução completaQuestão 92
Determine:
a)
Onde é a região entre os gráficos das funções e , com .
Ver solução completaQuestão 93
Calcule as integrais para as regiões indicadas:
a)
limitada por , e .
Ver solução completaQuestão 95
Calcule onde R é a região delimitada por . Desenhe a região R de integração.
Ver solução completaQuestão 96
1 – Considere a integral abaixo
a) esboce a região descrita nos limites de integração.
Ver solução completaQuestão 97
Determine:
b)
Onde é a região entre os gráficos das funções e , com .
Ver solução completaQuestão 105
Determine o volume do sólido limitado pelos planos coordenados e pelo plano .
Ver solução completaQuestão 106
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
c)
Ver solução completaQuestão 107
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
b)
Ver solução completaQuestão 108
Considere uma lâmina que ocupa a região planar que se encontra entre as curvas , e . Suponha que a densidade em um ponto qualquer na lâmina seja dada pela função . Determine a massa total da lâmina.
Ver solução completaQuestão 109
A integral fornece a área de uma região no plano . Esboce a região, identifique cada curva limite com sua equação, escreva as coordenadas dos pontos onde há intersecção das curvas. Depois encontre a área da região.
Ver solução completaQuestão 112
Escreva duas integrais iteradas correspondentes à integral dupla , onde é a região do plano limitada pelas curvas e .
Ver solução completaQuestão 114
, onde é a região do primeiro quadrante limitada pela circunferência de centro
e raio .
Ver solução completaQuestão 117
Sendo a região plana delimitada pelas curvas dadas pela equação e , calcule
Ver solução completaQuestão 118
Calcule as integrais:
a) , onde é o disco de centro na origem e raio .
Ver solução completaQuestão 119
Considere a região plana definida por
d) Calcule a área da região plana:
Ver solução completaQuestão 120
Determine o volume do sólido limitado pelos planos coordenados e pelo plano .
Ver solução completaQuestão 121
Determine o valor da integral dupla
Para o qual é o interior de um quadrado cujos vértices estão sobre os eixos coordenados
Ver solução completaQuestão 122
Calcule o fluxo de sobre a superfície fronteira do sólido delimitado pelo cilindro e os planos e .
Ver solução completaQuestão 123
Esboce a região como uma região do tipo e do tipo . Escreva as integrais possíveis e use uma delas para resolver
Onde é limitada pelas retas , e
Ver solução completaQuestão 127
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
07. , limitada pela parábola e pelas retas e .
Ver solução completaQuestão 128
Considere as regiões planas
Seja
- Esboce a região e identifique sua fronteira como uma curva clássica (ou seja, forneça seu nome e sua equação)
- Esboce o interior da região e determine-o através de desigualdades.
- Esboce a região e identifique sua fronteira como uma curva clássica (ou seja, forneça seu nome e sua equação)
- Esboce a região e, em seguida, descreva-a no seguinte formato:
Explicitando as constantes reais e e as funções e .
Ver solução completaQuestão 134
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
2 - , a região do primeiro quadrante dada por
Ver solução completaQuestão 135
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
1) , a região determinada pelas curvas e .
Ver solução completaQuestão 136
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
06. , a região retangular definida pelas desigualdades ,
Ver solução completaQuestão 137
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
03. , a região do primeiro quadrante definida por , .
Ver solução completaQuestão 139
04. , a região do primeiro quadrante, limitada pela reta e pelo arco da circunferência de raio , com centro no ponto .
Ver solução completaQuestão 140
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
05. , o triângulo com vértices nos pontos , e .
Ver solução completaQuestão 141
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
08. , a região definida por , .
Ver solução completaQuestão 142
Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida
9.
Ver solução completaQuestão 143
Se D é a região limitada pelas curvas e e se
Então podemos afirmar que
Ver solução completaQuestão 144
Calcule a área e faça um esboço do gráfico da região representada pela integral:
Ver solução completaQuestão 147
Esboce a região de integração e calcule a integral trocando a ordem de integração.
a)
Ver solução completaQuestão 148
Esboce a região de integração e calcule a integral trocando a ordem de integração.
b)
Ver solução completaQuestão 149
Calcule as integrais para as regiões indicadas:
c)
é a região triangular com vértices e
Ver solução completaQuestão 150
Calcule as integrais para as regiões indicadas:
d)
é limitada por e .
Ver solução completaQuestão 155
Encontre a área da região limitada pela parábola e pela reta utilizando integral dupla.
(a)
(b)
(c)
(d)
(e)
Ver solução completa