Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.5 - Ex. 10c

As populações médias de presas e de predadores são definidas por

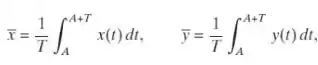
respectivamente, em que T é o período de um ciclo completo e A é uma constante não negativa arbitrária. Calcule outras soluções do sistema (2) — ou seja, soluções satisfazendo outras condições iniciais — e determine e para essas soluções. Os valores de e são os mesmos para todas as soluções?

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a trajetória a partir das equações. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser pegar as equações e arrumar a casa.

Do seno para o cosseno, temos o período igual a

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Só pelas derivadas, podemos ver que os valores médios crescem junto com a amplitude.

Resposta

Só pelas derivadas, podemos ver que os valores médios crescem junto com a amplitude.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o sistemaem que a e b são constantes positivas. Observe que esse sistema é o mesmo que o sistema do exemplo no texto quando a = 1 e b = 0,75. Suponha que as condições iniciais são x(0) = 5 e

As populações médias de presas e de predadores são definidas porrespectivamente, em que T é o período de um ciclo completo e A é uma constante não negativa arbitrária. Para a solução do sistema não li

Calcule outras soluções do sistema (2) — ou seja, soluções satisfazendo outras condições iniciais — e determine seus períodos. O período é o mesmo para todas as condições iniciais?

Considere o sistemaem que a, σ, α, c e γ são constantes positivas. . Descreva o efeito nas duas populações quando σ varia de zero a aγ/c.

Neste problema, vamos examinar a diferença de fase entre as variações cíclicas das populações de predadores e de presas dadas pelas Eqs. (24) desta seção. Vamos supor que K0 e que o tempo t é medido a